AK F.*ing leetcode 流浪计划之凸包

[LightningBilly]

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

@[toc]

零、简介

在计算几何类题目中，凸包是一个基础算法。应用主要有查找构成凸包的点，判定凸多边形，计算凸包的周长或面积。更高级的有利用旋转卡壳计算凸包的最远点对，面积最大的三角形，最小外接矩形，最小宽度。

本文结合凸包性质讲解求解凸包过程，以及旋转卡壳求解优化。

一、凸包定义及性质

凸包的定义

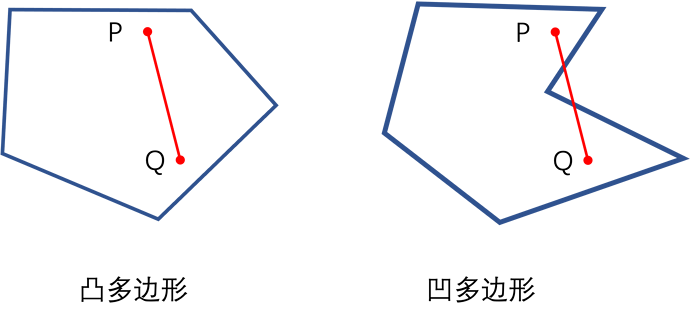
凸包(Convex Hull)定义为: 平面的一个子集S被称为是“凸”的,当且仅当对于任意两点p,s∈S,线段ps都完全属于S。

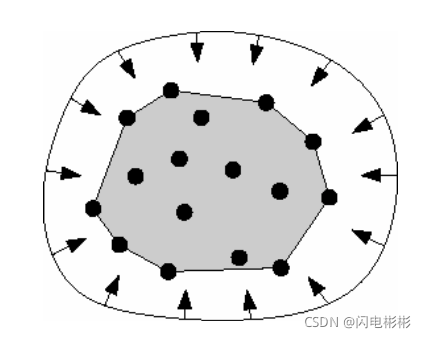
一种直观理解凸包的方法是，假想墙有很多钉子，然后用一根皮筋将所有钉子围住。当皮筋收缩时就会形成一个包围所有钉子的凸多边形。

凸包的性质

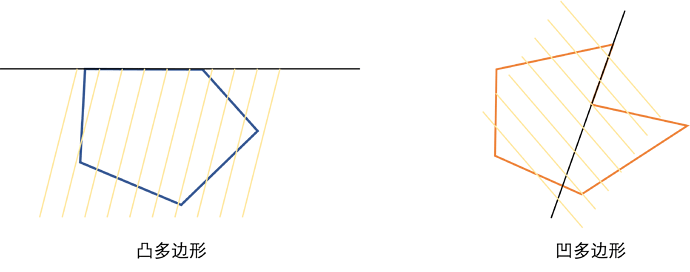
1 对于任选一条边所在的直线，凸包所有的点都在直线的同一侧。

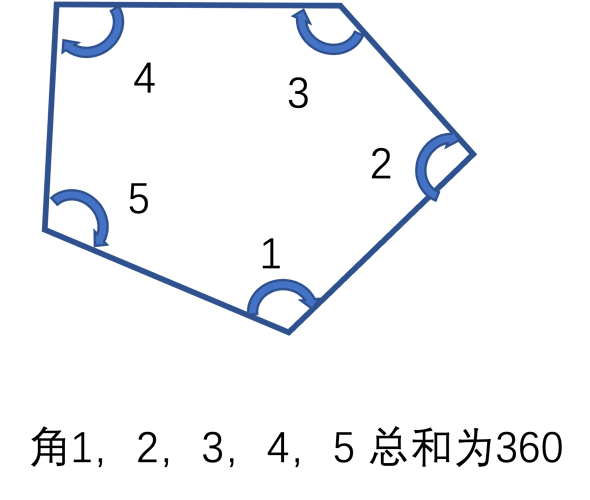
2 所有内角和等于360度。

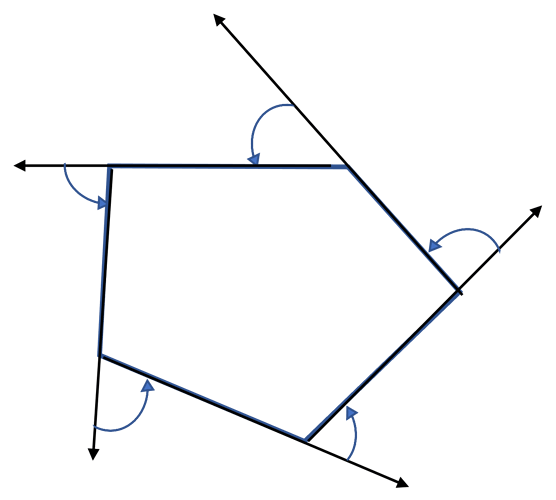
3 逆时针遍历所有边，下一条边都是在上一条边逆时针旋转方向上。

二、凸包求解过程

凸包求解是凸包相关的基本问题。
给定若干点，找到一个最小的凸多边形使得这个多边形包含所有的点。
参考题目：Problem - 1392
题目要求凸包周长。
先求出构成凸包的顶点，然后求线段长度即可。

求解算法

引用自 https://blog.csdn.net/qq_39826163/article/details/83861353
所用的方法名叫 Graham扫描法。
我们可以利用 上述性质3，创建一个栈，将点按逆时针加入到栈中，如果发现最近3点所组成线段不成逆时针，则去除最后一点。

算法步骤：

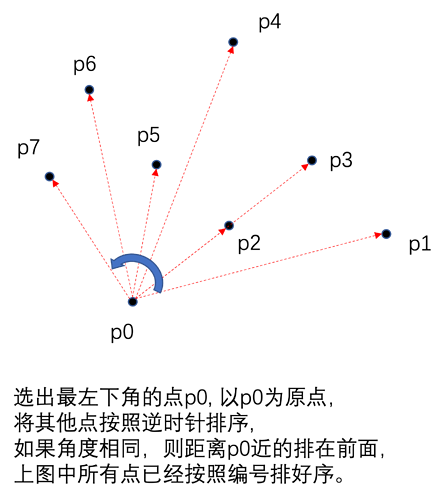
1. 对所有点进行排序
   
   
   
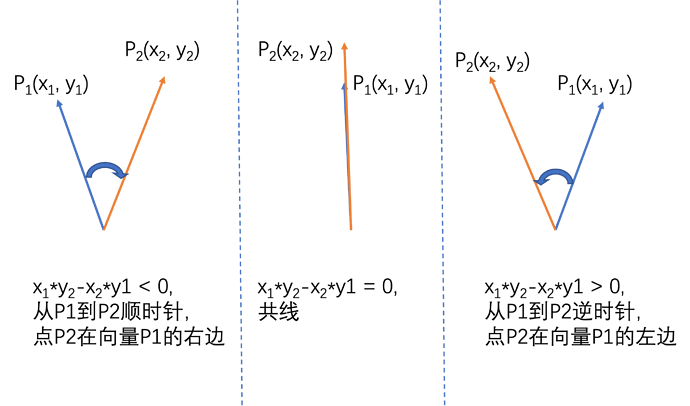
   在实际排序实现时可以使用向量的叉积。
   
   
2. 选点。
   
   

step 1 向栈中放入排好序的前2个点。
step 2 遍历接下来的所有点，如果发现栈中最后2个点与当前点不成逆时针，则把栈中最后一点出栈。
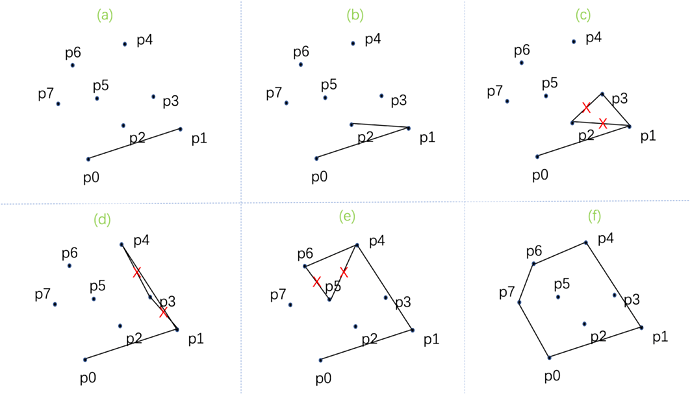
step 3 算法结束后，栈中所有点按逆时针排列成凸包所有顶点。相邻2点所组成的边就是凸包的边。

在上图 (c)中 向量（p2-p1）与（p3-p2）呈现顺时针，故将p2从栈中删除。(d), (e) 同理。

算法实现

参考题目：Problem - 1392
求凸包周长

#include <stdio.h>
#include <cmath>
#include <algorithm>

using namespace std;

const int M = 32767 + 10;

class Point {
public:
    int x, y;
};

int xmult(Point a, Point b, Point c) {
    b.x -= a.x;
    b.y -= a.y;
    c.x -= a.x;
    c.y -= a.y;

    return b.x * c.y - b.y * c.x;
}

int dis(Point a, Point b) {
    b.x -= a.x;
    b.y -= a.y;

    return b.x * b.x + b.y * b.y;
}

Point P[M];
Point lowPoint;
int ind[M];
int st[M];

bool cmp(int i, int j) {
    int m = xmult(lowPoint, P[i], P[j]);
    if (m != 0) {
        return m > 0;
    }
    return dis(lowPoint, P[i]) < dis(lowPoint, P[j]);
}

void solve() {
    int n;
    while (scanf("%d", &n) != EOF && n) {
        lowPoint.y = M; // 最低最左边的点
        for (int i = 0; i < n; ++i) {
            scanf("%d%d", &P[i].x, &P[i].y);
            ind[i] = i;
            if (P[i].y < lowPoint.y || (P[i].y == lowPoint.y && P[i].x < lowPoint.x)) lowPoint = P[i];
        }
        if (n == 1) {
            puts("0.00");
            continue;
        } else if (n == 2) {
            printf("%.2f\n", sqrt(dis(P[0], P[1])));
            continue;
        }

        sort(ind, ind + n, cmp);
        /*
        puts("");
        for (int i = 0; i < n; ++i) {
            printf("%d %d %d\n", P[ind[i]].x, P[ind[i]].y, ind[i]);
        }
        puts("");
         */

        int top = 2;
        st[0] = ind[0];
        st[1] = ind[1];
        for (int i = 2; i < n; ++i) {
            while (top >= 2 && xmult(P[st[top - 2]], P[ind[i]], P[st[top - 1]]) >= 0) {
                top--;
            }
            st[top++] = ind[i];
        }
        st[top++] = ind[0];
        double ans = 0;

        for (int i = 0; i < top - 1; ++i) {
            ans += sqrt(dis(P[st[i]], P[st[i + 1]]));
            // printf("%d %d\n", P[st[i]].x, P[st[i]].y);
        }
        printf("%.2f\n", ans);
    }
}

int main(void) {
    // int a=32767;
    // printf("%d\n", a*a*2);
    // printf("%d\n", (1<<30)-1+(1<<30));
    solve();

    return 0;
}

/*
5
0 0
0 4
4 0
4 4
2 2

9
12 7
24 9
30 5
41 9
80 7
50 87
22 9
45 1
50 7
 */

三、旋转卡壳及其应用

旋转卡壳的历史，可以自己找资料看。
这里只介绍一下比较常见的应用，及算法思路优化。

基本问题

已知一个凸包的所有边，求凸包中每条边所对应最远距离的点。
旋转卡壳形象的说就是用一个卡尺去把多边形夹住，当卡尺的一边与多边形的边重合时，另一边也会对应到一个最远点。

朴素做法

一种相素做法就是枚举。

for 所有边 {
	for 所有点{
		检查点与边组成三解形面积是否大于候选答案，是就更新答案。
	}
}

这种做法的复杂度是O(n^2)

单峰特性优化

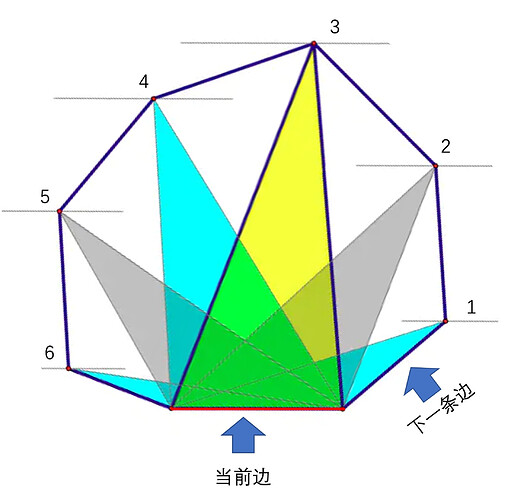
对单一遍历过程观察。

对于红色边来说，从点1，2，3是一直增大的，到了4就开始减少了，所以最佳点是3，可以发现是一个单峰函数，就是说我们不用遍历所有点，如果发现开始下降了，那么当前点就是最佳点了。
到了下一条边，最佳点肯定是从前一条边的最佳点开始找。
对于下一条边来说，2，3点还处于上升状态，所以从3开始往后找，不会错过最佳点。
这样的特性可以使用双指针法，做到O(n)复杂度。

算法实现

参考题目：2187 -- Beauty Contest
题目是让求所有点中距离最远的点对距离（输出平方即可）。
肯定在凸包上，先求出凸包。
最远点对肯定在某一边对应的最远点上。

#include <stdio.h>
#include <iostream>
#include <cmath>
#include <algorithm>

using namespace std;

# define PI acos(-1.0)
const int M = 1e6+10;

const double eps = 1e-6;

int cmpDouble(double a, double b) {
    if (fabs(a-b)< eps) return 0;
    if (a<b) return -1;
    return 1;
}

class Point {
public:
    int x, y;
    Point(int a, int b):x(a), y(b){}
    Point(){}

    Point operator - (Point p) const {
        return Point(x-p.x, y-p.y);
    }

    Point operator + (Point p) const {
        return Point(x+p.x, y+p.y);
    }

    // 点积
    int operator * (Point p) const {
        return x*p.x + y*p.y;
    }

    // 叉积
    int operator ^ (Point p) const {
        return x*p.y - y*p.x;
    }

    int dis() const {
        return x*x+y*y;
    }
};
/*
int operator ^ (Point a, Point b) {
    return a.x*b.y-a.y*b.x;
}
*/
Point points[M];
Point lowPoint;
int st[M], top;

bool cmp(Point p1, Point p2) {
    p1 = p1-lowPoint;
    p2 = p2-lowPoint;

    int xmult =p1^p2; // 求叉积
    if (xmult!=0) {
        return xmult > 0;
    }

    return p1.dis()<p2.dis();
}

void graham(int n) {
    lowPoint = points[0];
    for (int j = 0; j < n; ++j) {
        if(points[j].y<lowPoint.y || (points[j].y==lowPoint.y && points[j].x<lowPoint.x)) lowPoint = points[j];
    }
    sort(points, points+n, cmp);
    top=2;
    st[0]=0;
    st[1]=1;

    for (int i = 2; i < n; ++i) {
        while(top>2 && ((points[st[top-1]]-points[st[top-2]])^(points[i]-points[st[top-1]]))<=0)top--;
        st[top++]=i;
    }
}

int rotate() {
    st[top]=st[0]; // 将第一点连接后最后，作为最后一条边的终点
    int up = 1;
    int ans = -1;

    for (int i = 0; i < top; ++i) {
        Point bottom = points[st[i+1]] - points[st[i]];
        // 以i, i+1 线段为底
        // 查看顶部最高点, 发现下一个点比当前点高，就+1
        while(abs(bottom^(points[st[up]]-points[st[i]]))<abs(bottom^(points[st[up+1]]-points[st[i]]))) up = (up+1)%top;
        // 将顶部与底部2个点分别求。 要考虑顶点处于平行线上的情况。这里利用对角顶。
        ans = max(ans, (points[st[up]]-points[st[i]]).dis());
        ans = max(ans, (points[st[up+1]]-points[st[i+1]]).dis());
    }

    return ans;
}

void solve() {
    int N;
    scanf("%d", &N);

    for (int i = 0; i < N; ++i) {
        scanf("%d%d", &points[i].x, &points[i].y);
    }

    graham(N);
    int ans = rotate();
    printf("%d\n", ans);
}



int main(void) {
    solve();
    return 0;
}

四、牛刀小试

练习1 求解凸包（可共线）

安装栅栏- https://leetcode-cn.com/problems/erect-the-fence/

题目大意

在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。

示例 1:

输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]
解释:

示例 2:

输入: [[1,2],[2,2],[4,2]]
输出: [[1,2],[2,2],[4,2]]
解释:

即使树都在一条直线上，你也需要先用绳子包围它们。

注意:

所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
输入的整数在 0 到 100 之间。
花园至少有一棵树。
所有树的坐标都是不同的。
输入的点没有顺序。输出顺序也没有要求。

题目解析

凸包求解。
与模板有一点小区别：

1. 共线的点可以选入。
2. 少于3个点需要特殊处理。

共线处理方法：
前面选择点时，判断条件由原来 必须逆时针转改成逆时针或共线。
共线的点只可能出现在开始或末尾，开始的点本来就是从近到远排序的，所以会被选进来。需要处理的是最后几个点。
在选择完所有的点后，需要判断最后面的点是不是与最后一条线段共线。

AC代码

type Point []int

var LowPoint Point

type PointList [][]int

func (x PointList) Len() int { return len(x) }
func (x PointList) Less(i, j int) bool {
	xm := xmult(LowPoint, x[i], x[j])
	if xm != 0 {
		return xm > 0
	}
	return dism(x[i], LowPoint) < dism(x[j], LowPoint)
}
func (x PointList) Swap(i, j int) { x[i], x[j] = x[j], x[i] }

// 求解叉积，>0 代表逆时针转，=0代表共线
func xmult(a, b, c Point) int {
	d1 := Point{b[0] - a[0], b[1] - a[1]}
	d2 := Point{c[0] - a[0], c[1] - a[1]}

	return d1[0]*d2[1] - d1[1]*d2[0]
}

func dism(a, b Point) int {
	return (b[0]-a[0])*(b[0]-a[0]) + (b[1]-a[1])*(b[1]-a[1])
}

func outerTrees(trees [][]int) [][]int {
	if len(trees)<=3 {
		return trees
	}
	// 查找最左下解的点
	LowPoint = trees[0]
	for _, tree := range trees {
		if tree[1] < LowPoint[1] || (tree[1] == LowPoint[1] && tree[0] < LowPoint[0]) {
			LowPoint = tree
		}
	}

	sort.Sort(PointList(trees))

	stack := []int{0, 1}
	for i := 2; i < len(trees); i++ {
		for len(stack) > 1 && xmult(trees[stack[len(stack)-2]], trees[stack[len(stack)-1]], trees[i]) < 0 {
			stack = stack[:len(stack)-1]
		}
		stack = append(stack, i)
	}

	// 取凸包里的最后一个点，将排序的最后几个点进行比较是不是与最后一条线共线
	last := -1
	// 必须大于3个点，且凸包不是一条线。
	if len(stack) > 2 && xmult(trees[stack[0]], trees[stack[1]], trees[stack[len(stack)-1]]) > 0 {
		last = stack[len(stack)-1]
	}

	for i := last-1; i > 0 && last >= 0; i-- {
		if xmult(trees[stack[0]], trees[i], trees[last]) == 0 {
			stack = append(stack, i)
		}
	}

	ans := [][]int{}
	for _, n:= range stack {
		ans = append(ans, trees[n])
	}

	return ans
}

练习2 求解最小面积包围矩形

矩形面积- http://acm.hdu.edu.cn/showproblem.php?pid=5251

题目大意

小度熊有一个桌面，小度熊剪了很多矩形放在桌面上，小度熊想知道能把这些矩形包围起来的面积最小的矩形的面积是多少。

题目解析

最小矩形桌面上的矩形顶点就可以了。
等价于包围由顶点所组成的凸包。
先求出凸包，再求出最小矩形。

简单可以证明，最小矩形的某一边肯定会与凸包的一边共线，如果不共线肯定可以转动，一转动矩形面积就变小了。
只要遍历所有的边，以该边为矩形的一边所在位置。然后构造矩形。

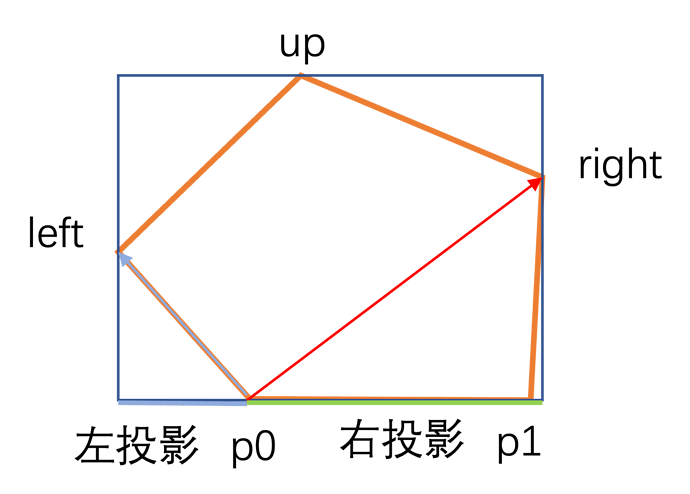
对于某一条边p0-p1可以找一个最顶点up, 最左边left, 最右边right。
利用 向量叉积是平行四边形面积公式计算出高。
利用投影公式算出左投影，右投影的距离。
D = |p1-p0|
H=abs((p1-p0)X(up-p0))/D，X代表叉积
根据公式 ab = |a||b|cos∂ → 在向量a上投影为ab/|a|
右投影=(p1-p0)*(right-p0)/D, 星号是点积。
投影的计算也是单峰分布的，所以和最高点计算类似，具体看代码，计算left第第一次要在left计算完后再开始（一开始是先增大再减小，再增大）。

AC代码

#include <stdio.h>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <random>

using namespace std;

# define PI acos(-1.0)
const int M = 1e6+10;

const double eps = 1e-6;

int cmpDouble(double a, double b) {
    if (fabs(a-b)< eps) return 0;
    if (a<b) return -1;
    return 1;
}

class Point {
public:
    int x, y;
    Point(int a, int b):x(a), y(b){}
    Point(){}

    Point operator - (Point p) const {
        return Point(x-p.x, y-p.y);
    }

    Point operator + (Point p) const {
        return Point(x+p.x, y+p.y);
    }

    // 点积
    int operator * (Point p) const {
        return x*p.x + y*p.y;
    }

    // 叉积
    int operator ^ (Point p) const {
        return x*p.y - y*p.x;
    }

    int dis() const {
        return x*x+y*y;
    }

    string String() const {
        return to_string(x)+","+to_string(y);
    }
};
/*
int operator ^ (Point a, Point b) {
    return a.x*b.y-a.y*b.x;
}
*/
Point points[M];
Point lowPoint;
int st[M], top;

bool cmp(Point p1, Point p2) {
    p1 = p1-lowPoint;
    p2 = p2-lowPoint;

    int xmult =p1^p2;
    if (xmult!=0) {
        return xmult > 0;
    }

    return p1.dis()<p2.dis();
}

void graham(int n) {
    lowPoint = points[0];
    for (int j = 0; j < n; ++j) {
        if(points[j].y<lowPoint.y || (points[j].y==lowPoint.y && points[j].x<lowPoint.x)) lowPoint = points[j];
    }
    sort(points, points+n, cmp);
    top=2;
    st[0]=0;
    st[1]=1;

    for (int i = 2; i < n; ++i) {
        while(top>2 && ((points[st[top-1]]-points[st[top-2]])^(points[i]-points[st[top-1]]))<=0)top--;
        st[top++]=i;
    }
}

double rotate() {
    st[top]=st[0];
    int up = 1;
    int left = 1, right=1;
    double ans = -1;

    for (int i = 0; i < top; ++i) {
        Point bottom = points[st[i+1]] - points[st[i]];
        // 以i, i+1 线段为底
        // 查看顶部最高点
        while(abs(bottom^(points[st[up]]-points[st[i]]))<abs(bottom^(points[st[up+1]]-points[st[i]]))) up = (up+1)%top;
        while((bottom*(points[st[right]]-points[st[i]]))<(bottom*(points[st[right+1]]-points[st[i]]))) right = (right+1)%top;
        if (i==0) left=right;
        while((bottom*(points[st[left+1]]-points[st[i]]))<=(bottom*(points[st[left]]-points[st[i]]))) left = (left+1)%top;

        double D = sqrt(bottom.dis());

        double L = bottom*(points[st[left]]-points[st[i]])/D;
        double R = bottom*(points[st[right]]-points[st[i]])/D;
        double W = R-L;
        double H = abs(bottom^(points[st[up]]-points[st[i]]))*1.0/D;
        double temp = W*H;

        if(ans <0 || cmpDouble(temp, ans)<=0) ans = temp;
    }

    return ans;
}

void solve() {
    int T;
    scanf("%d", &T);

    for (int k = 0; k < T; ++k) {
        int N;
        scanf("%d", &N);
        N*=4;

        for (int i = 0; i < N; ++i) {
            scanf("%d%d", &points[i].x, &points[i].y);
        }

        graham(N);
        double ans = rotate();
        printf("Case #%d:\n", k+1);
        printf("%.0f\n", ans);
    }
}



int main(void) {
    solve();
    return 0;
}

/*
2
 1
 0 0 1 0 1 1 0 1
 */

五、总结

1. 本文详细介绍了凸包求解方法，旋转卡壳原理及其应用。

2. 作用：基本应用求解凸包，旋转卡壳算法是在凸包基础上利用单峰性质做到O(n) 求外接圆，外接矩形，最远点对。

3. 在计算过程中，尽量减少浮点型运算，而转化为整型去处，可以提高计算效率与精度。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

六、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动手把刚才的题A了。

1. 凸包周长：Problem - 1392
2. 求凸包点（可共线）： 力扣
3. 求最远点对距离：2187 -- Beauty Contest
4. 最小包围矩形：Problem - 5251

---

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

hdu

以下将序号替换就是题目链接。

1. Problem - 1392
2. Problem - 1348
3. Problem - 2202
4. Problem - 5251

Poj

以下将序号替换就是题目链接。

1. 2187 -- Beauty Contest

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。