AK F.*ing leetcode 流浪计划之平面多边形交判断

LightningBilly · 2021 年11 月 17 日 02:09

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：判断2平面多边形是否相交
本文提到的多边形为普通多边（内部没有洞）。

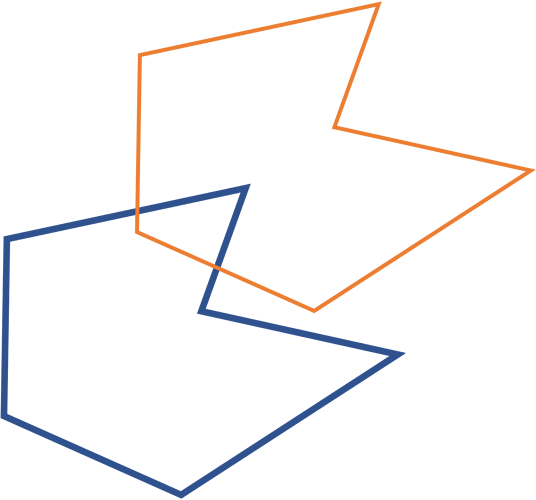
多边形之间情形

多边形有交说明2多边形之间有公共区域面积大于0。
总结起来以下三种情况：

边相交

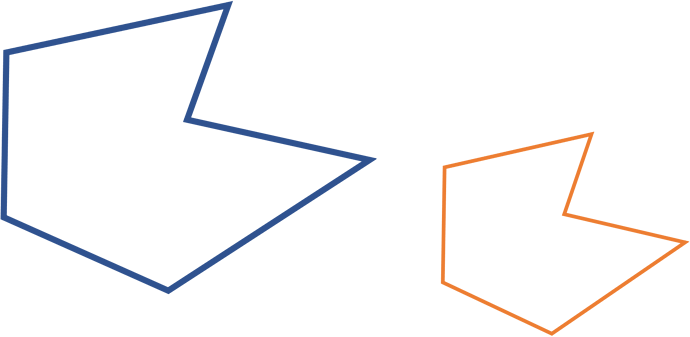
包含

包含有两种情况，完全重合与全包含。这种情况需要判断某一点是否在多边形内。

相离

从上面几种情况可以看出，判断多边形相交的2个条件：

有边相交
多边形内部某一点在另一个多边形内部

以上条件有一个满足即可。
下面来看如何判断边相交，某一点是否在多边形内部。

判断边是否相交

求值法

2条边是2个直线方程，代入解出一个点(x ,y) 检查该是否在线段范围内即可。
该方法明显比较麻烦，而且会涉及到浮点型计算，会影响速度与精度。

跨立测试

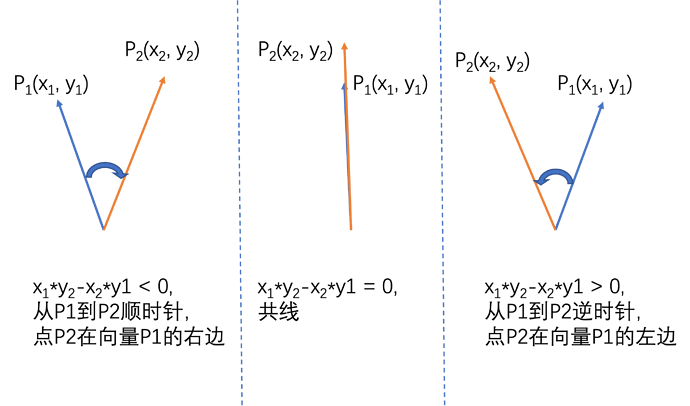
向量叉积特性

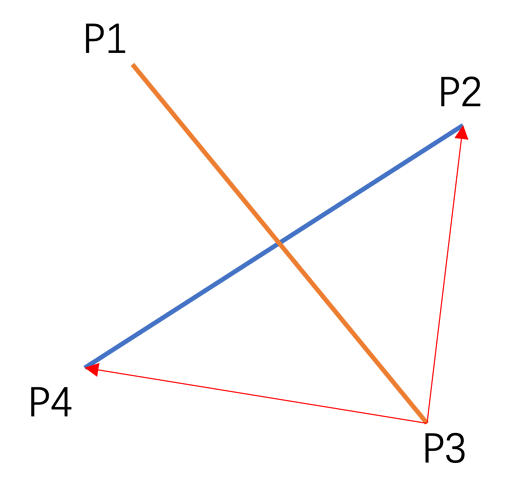
根据上述性质就可以判断一根线段的两端是否处在另一条线段的两侧。

只要计算向量 (P1-P3)*(P4-P3), (P1-P3)*(P2-P3), 判断它们是不是异号，即可知道P4, P2 是不是在线段P1P3的2侧。对线段P2P4也做同样的测试。
该方法只涉及到整数计算。

判断点是否在多边形内

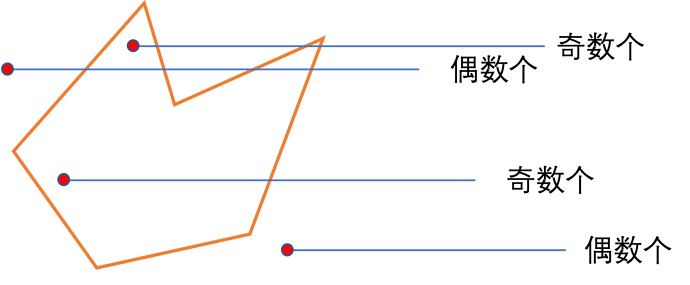
射线法：
从点出发平等于X轴向右发射一条射线，统计边与射线的交点，如果是奇数个就是在多边形内，如果是偶数就不在。

特殊情况

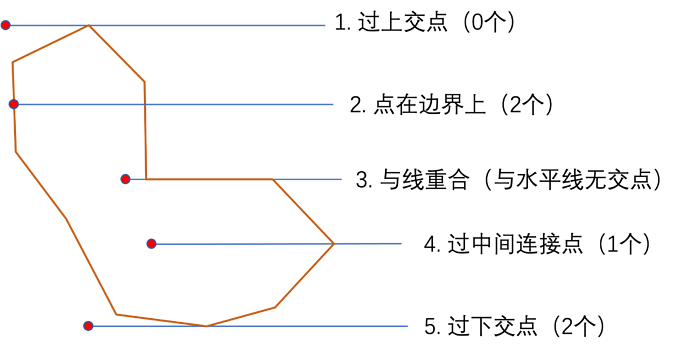
我们认为一条线段的上端点是空的，下端点为实的。基于此我们得到5种情况的交点数量。
如上图所示，
情况1，射线与线段上交点相交，由于上端点为空，交点个数为0
情况2，点在边界上，这种情况根据实际情况规定是否在多边形内
情况3，射线与边重合，此时规定与边无交点
情况4，射线与边相交于中间交点，一实一空，总数为1
情况5，相交于下端点，有2个交点

算法过程

dot = 0
for 所有边 {
	1. 通过叉积检查点是否处于边的左边
	2. 如果叉积为0则检测是否在边界上，做特殊处理
	3. 检测边是否与射线平行
	4. 检测上下端点是否处于射线上下
	根据以上条件决定dot是否+1
}
判断dot是否为奇数

算法实现

题目链接：Cupid’s Arrow - Problem - 1756

#include <stdio.h>

using namespace std;

# define PI acos(-1.0)

const int M = 1e6 + 10;

class Point {
public:
    int x, y;
};

Point P[M];

// 计算叉积
int xmult(Point a, Point b, Point c) {
    b.x -= a.x;
    b.y -= a.y;
    c.x -= a.x;
    c.y -= a.y;

    return b.x * c.y - b.y * c.x;
}

/* 判断射线与线段的交点情况
 * 0 无关，1 与射线相交，2 点落在线上
 */
int insect(Point p, Point p1, Point p2) {
    if (p1.y<p2.y) return insect(p, p2, p1);
    if(p1.y==p2.y && p2.x<p1.x) {
        return insect(p, p2, p1);
    }

    int m = xmult(p2, p1, p);
    if(m<0) return 0;
    if (m==0) { // 共线，有可能在边界，也有可能在线段外
        if (p1.y>=p.y && p2.y<=p.y && p1.x<=p.x && p.x<=p2.x) return 2;
        return 0;
    }

    if (p1.y>p.y && p.y>= p2.y) return 1; // 上端是空的，所以不能等

    return 0;
}

void solve() {
    int N;
    while(scanf("%d", &N)!=EOF) {
        for (int i = 0; i < N; ++i) {
            scanf("%d%d", &P[i].x, &P[i].y);
        }
        P[N]=P[0];
        int Q;
        scanf("%d", &Q);
        while(Q--) {
            Point p;
            scanf("%d%d", &p.x, &p.y);
            bool res = false;
            for (int i = 0; i < N; ++i) {
                int ins = insect(p, P[i], P[i+1]);
                if(ins==2) { // 此题规定边界算在多边形内
                    res = true;
                    break;
                }
                res ^= ins;
            }

            if (res)puts("Yes");
            else puts("No");
        }
    }
}

int main(void) {
    solve();

    return 0;
}

/*
12
1 1
2 3
3 3
 3 2
 4 2
 4 3
 5 1
 4 0
 3 0
 3 1
 2 1
 2 0
10
 0 1
 1 1
 1 2
 2 3
 2 2
 3 2
 3 5
 6 1
 5 0
 4 1


 4
 1 2
 2 3
 3 2
 1 2

 1
 2 2

 */

判断多边形相交

算法过程

for 一个多边形所有边 {
	for 另一个多边形所有边{
		如果相交 return true
	}
}

取一多边形内一点，判断是否在另一多边形内
取另一多边形内一点，判断是否在另一多边形内

算法实现

参考题目1：力扣

func xmult(p, p2, p3 []int) int {
	tp1 := []int{p2[0]-p[0], p2[1]-p[1]}
	tp2 := []int{p3[0]-p[0], p3[1]-p[1]}

	if tp1[0] * tp2[1]>tp1[1]*tp2[0] {return 1}
	if tp1[0] * tp2[1]<tp1[1]*tp2[0] {return -1}
	return 0
}

func insect(p1, p2, p3, p4 []int) bool {
	if xmult(p2, p1, p3) * xmult(p2, p1, p4)<0 && xmult(p4, p3, p1) * xmult(p4, p3, p2)<0 {return true}
	return false
}


func pInR(p []int, rec []int) bool {
	return rec[0]<p[0] && p[0]<rec[2] && rec[1]<p[1] && p[1]<rec[3]
}

func floatPinR(p []float64, rec []float64) bool {
	return rec[0]<p[0] && p[0]<rec[2] && rec[1]<p[1] && p[1]<rec[3]
}

func r1InR2(rec1 []int, rec2 []int) bool {
	// 检查一点是否在另一个矩形中
	if floatPinR([]float64{float64(rec1[0])+0.5, float64(rec1[1])+0.5},
		[]float64{float64(rec2[0]), float64(rec2[1]),float64(rec2[2]),float64(rec2[3])}) {
		return true
	}
	
	// 横线与竖线检查，竖线与横线检查
	if insect([]int{rec1[0], rec1[1]}, []int{rec1[0], rec1[3]}, []int{rec2[0], rec2[1]}, []int{rec2[2], rec2[1]}) {
		return true
	}
	if insect([]int{rec1[0], rec1[1]}, []int{rec1[0], rec1[3]}, []int{rec2[0], rec2[3]}, []int{rec2[2], rec2[3]}) {
		return true
	}


	if insect([]int{rec1[2], rec1[1]}, []int{rec1[2], rec1[3]}, []int{rec2[0], rec2[1]}, []int{rec2[2], rec2[1]}) {
		return true
	}
	if insect([]int{rec1[2], rec1[1]}, []int{rec1[2], rec1[3]}, []int{rec2[0], rec2[3]}, []int{rec2[2], rec2[3]}) {
		return true
	}


	if insect([]int{rec2[0], rec2[1]}, []int{rec2[0], rec2[3]}, []int{rec1[0], rec1[1]}, []int{rec1[2], rec1[1]}) {
		return true
	}
	if insect([]int{rec2[0], rec2[1]}, []int{rec2[0], rec2[3]}, []int{rec1[0], rec1[3]}, []int{rec1[2], rec1[3]}) {
		return true
	}


	if insect([]int{rec2[2], rec2[1]}, []int{rec2[2], rec2[3]}, []int{rec1[0], rec1[1]}, []int{rec1[2], rec1[1]}) {
		return true
	}
	if insect([]int{rec2[2], rec2[1]}, []int{rec2[2], rec2[3]}, []int{rec1[0], rec1[3]}, []int{rec1[2], rec1[3]}) {
		return true
	}


	return false
}

func isRectangleOverlap(rec1 []int, rec2 []int) bool {
	return r1InR2(rec1, rec2) || r1InR2(rec2, rec1)
}

参考题目2：力扣


func max(a,b int) int {
	if a > b{
		return a
	}
	return b
}


func min(a,b int) int {
	if a < b{
		return a
	}
	return b
}


func xmult(p, p2, p3 []int) int {
	tp1 := []int{p2[0]-p[0], p2[1]-p[1]}
	tp2 := []int{p3[0]-p[0], p3[1]-p[1]}

	if tp1[0] * tp2[1]>tp1[1]*tp2[0] {return 1}
	if tp1[0] * tp2[1]<tp1[1]*tp2[0] {return -1}
	return 0
}

func insect(p1, p2, p3, p4 []int) bool {
	if xmult(p2, p1, p3) * xmult(p2, p1, p4)<0 && xmult(p4, p3, p1) * xmult(p4, p3, p2)<0 {return true}
	return false
}


func pInR(p []int, rec []int) bool {
	return rec[0]<p[0] && p[0]<rec[2] && rec[1]<p[1] && p[1]<rec[3]
}

func floatPinR(p []float64, rec []float64) bool {
	return rec[0]<p[0] && p[0]<rec[2] && rec[1]<p[1] && p[1]<rec[3]
}

func r1InR2(rec1 []int, rec2 []int) bool {
	if floatPinR([]float64{float64(rec1[0])+0.5, float64(rec1[1])+0.5},
		[]float64{float64(rec2[0]), float64(rec2[1]),float64(rec2[2]),float64(rec2[3])}) {
		return true
	}
	if insect([]int{rec1[0], rec1[1]}, []int{rec1[0], rec1[3]}, []int{rec2[0], rec2[1]}, []int{rec2[2], rec2[1]}) {
		return true
	}
	if insect([]int{rec1[0], rec1[1]}, []int{rec1[0], rec1[3]}, []int{rec2[0], rec2[3]}, []int{rec2[2], rec2[3]}) {
		return true
	}


	if insect([]int{rec1[2], rec1[1]}, []int{rec1[2], rec1[3]}, []int{rec2[0], rec2[1]}, []int{rec2[2], rec2[1]}) {
		return true
	}
	if insect([]int{rec1[2], rec1[1]}, []int{rec1[2], rec1[3]}, []int{rec2[0], rec2[3]}, []int{rec2[2], rec2[3]}) {
		return true
	}


	if insect([]int{rec2[0], rec2[1]}, []int{rec2[0], rec2[3]}, []int{rec1[0], rec1[1]}, []int{rec1[2], rec1[1]}) {
		return true
	}
	if insect([]int{rec2[0], rec2[1]}, []int{rec2[0], rec2[3]}, []int{rec1[0], rec1[3]}, []int{rec1[2], rec1[3]}) {
		return true
	}


	if insect([]int{rec2[2], rec2[1]}, []int{rec2[2], rec2[3]}, []int{rec1[0], rec1[1]}, []int{rec1[2], rec1[1]}) {
		return true
	}
	if insect([]int{rec2[2], rec2[1]}, []int{rec2[2], rec2[3]}, []int{rec1[0], rec1[3]}, []int{rec1[2], rec1[3]}) {
		return true
	}


	return false
}

func isRectangleOverlap(rec1 []int, rec2 []int) bool {
	return r1InR2(rec1, rec2) || r1InR2(rec2, rec1)
}

func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
	// 先计算出总面积
	area := (ax2-ax1)*(ay2-ay1) + (bx2-bx1)*(by2-by1)

	// 先判断是否有相交区域
	if !isRectangleOverlap([]int{ax1, ay1, ax2, ay2}, []int{bx1, by1, bx2, by2}) {return area}

	// 计算出上、下、左、右
	High := min(ay2, by2)
	Low := max(ay1, by1)
	Left := max(ax1, bx1)
	Right := min(ax2, bx2)
	W := Right-Left
	H := High-Low
	
	// 减去一个相交区域面积
	return area - W*H
}

在这里插入图片描述