AK F.*ing leetcode 流浪计划之Bresenham画线

算法之美
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

基本变量定义

P1, P2 为要画线段的起终点，P1 = (x1, y1),P2 = (x2, y2)
∆x = x2-x1, ∆y = y2-y1,
m代表直线斜率0<m<1, m = ∆y/∆x
直线方程 y = mx+b

Bresenham 推导过程及实现

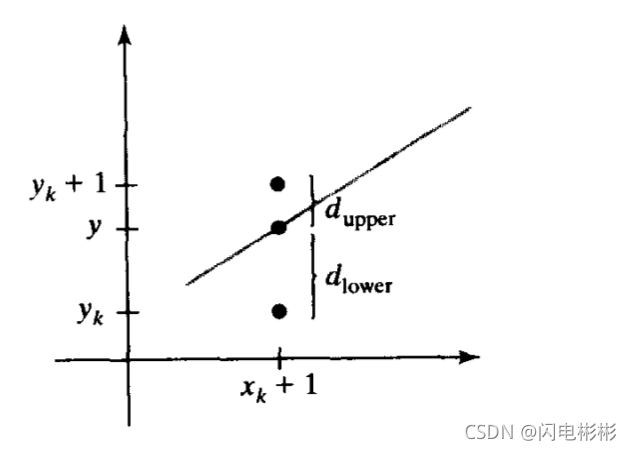
在这里插入图片描述

假设当前已经画到点 Pc(x_k, y_k), 则下一个点只有2种可能(x_k+1, y_k) 或(x_k+1, y_k+1)

y 是直线上x_k+1 所对应实际的坐标

y=m (x_k+1)+b

令d_{upper} = y_k+1 - y = y_k+1-m(x_k+1)-b

d_{lower} = y-y_k = m (x_k+1)+b-y_k

d_{lower}-d_{upper} = 2m(x_k+1)-2y_k+2b-1

p_k是决策参数

令p_k = ∆x(d_{lower}-d_{upper}), 由于m = ∆y/∆x

代入式子

p_k = 2∆y(x_k+1)-2∆x*y_k+2∆x*b-∆x

= 2∆y*x_k-2∆x*y_k+2∆y+∆x(2b-1)

当p_k<0时，说明y_k离y更近，就取y_k; 否则，y_k+1离y更近，取y_k+1.
到此为止我们已经得到下一个点的决策参数。只要依次计算就可以得到所线上的坐标。但是pk的计算中有很多乘法，比较耗时，我们可以通过步进法将其转化成加法来做。具体如下：
将x_{k+1}, y_{k+1}代入式子，可得到

p_{k+1}=2∆y(x_{k+1})-2∆x*y_{k+1}+2∆x*b-∆x

x_{k+1}=x_k+1则p_{k+1}-p_k = 2∆y-2∆x(y_{k+1}-y_k)

移项得p_{k+1} =p_k+ 2∆y-2∆x(y_{k+1}-y_k),

这样我们就得到p_k的递推式。

p_{k+1} =p_k+ 2∆y+\begin{cases} -2∆x, p_k>=0 \\ 0, p_k<0\end{cases}

上述算法中2∆x, 2∆y都可以事先算好，后续只要用到加法即可
p0计算
将(x_0,y_0)代入p_k表达式得：

p_0 = 2∆y*x_0-2∆x*y_0+2∆y+∆x(2b-1)

又因为 y_0 = m*x_0+b= ∆y/∆x*x_0+b, 代入上式得：

p_0 = 2∆y*x_0-2∆x*(∆y/∆x*x_0+b)+2∆y+∆x(2b-1)

=2∆y*x_0-2∆y*x_0-2∆x*b+2∆y+∆x(2b-1)

= 2∆y-∆x

上述只是讲了0<m<1的算法，对于-1<m<0可以直接对称过去。
对于|m|>1的情况可以把x,y 互换。
对于m=0, 无穷大的情况也适用。

代码实现

#include "glew/2.2.0_1/include/GL/glew.h"
#include "glfw/3.3.4/include/GLFW/glfw3.h"
#include <iostream>
using namespace std;


void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode)
{
    //如果按下ESC，把windowShouldClose设置为True，外面的循环会关闭应用
    if(key==GLFW_KEY_ESCAPE && action == GLFW_PRESS)
        glfwSetWindowShouldClose(window, GL_TRUE);
    std::cout<<"ESC"<<mode;
}



class Point {
public:
    int x, y;
    Point(int xx, int yy):x(xx), y(yy){}
};

void setPixel(Point p) {
    // cout<<p.x<<","<<p.y<<endl;
    glBegin(GL_POINTS);
    glVertex2i(p.x, p.y);
    glEnd();
    glFlush();
}


/*
 * 简单Bresenham 算法
 * 只处理|m|>1
 */
void LineBres_2(Point p1, Point p2) {
	// 保持从下往上画
    if(p2.y<p1.y) {
        Point t = p2;
        p2=p1;
        p1=t;
    }

    int deltaX = abs(p2.x-p1.x), deltaY = abs(p2.y-p1.y);
    int p0 = 2*deltaX-deltaY;
    int twDeltaX = 2*deltaX, twDeltaXmTwoDeltaY = 2*deltaX-2*deltaY;
    int step = 0;
    if(deltaX>0) step = (p2.x-p1.x) / deltaX;
    setPixel(p1);
    for (; p1.y < p2.y;) {
        p1.y++;
        if(p0<0) {
            p0+=twDeltaX;
        } else {
            p0+=twDeltaXmTwoDeltaY;
            p1.x+=step;
        }
        setPixel(p1);
        cout<<p1.x<<","<<p1.y<<endl;
    }

}

/*
 * 简单Bresenham 算法
 * 只处理|m|<=1
 */
void LineBres_1(Point p1, Point p2) {
	// 保持从左到右画
    if(p2.x<p1.x) {
        Point t = p2;
        p2=p1;
        p1=t;
    }

    int deltaX = abs(p2.x-p1.x), deltaY = abs(p2.y-p1.y);
    if(deltaX<deltaY) {
        LineBres_2(p1, p2);
        return;
    }
    int p0 = 2*deltaY-deltaX;
    int twDeltaY = 2*deltaY, twDeltaYmTwoDeltaX = 2*deltaY-2*deltaX;
    int step = 0;
    if(deltaY>0) step = (p2.y-p1.y) / deltaY;
    setPixel(p1);
    for (; p1.x < p2.x;) {
        p1.x++;
        if(p0<0) {
            p0+=twDeltaY;
        } else {
            p0+=twDeltaYmTwoDeltaX;
            p1.y+=step;
        }
        setPixel(p1);
        cout<<p1.x<<","<<p1.y<<endl;
    }

}


int main(void) {
    //初始化GLFW库
    if (!glfwInit())
        return -1;
    //创建窗口以及上下文
    GLFWwindow *window = glfwCreateWindow(400, 400, "hello world", NULL, NULL);
    if (!window) {
        //创建失败会返回NULL
        glfwTerminate();
    }

    //建立当前窗口的上下文
    glfwMakeContextCurrent(window);

    glfwSetKeyCallback(window, key_callback); //注册回调函数
    //glViewport(0, 0, 400, 400);
    gluOrtho2D(-200, 200.0, -200, 200.0);
    //循环，直到用户关闭窗口
    cout<<123<<endl;
    while (!glfwWindowShouldClose(window)) {
        /*******轮询事件*******/
        glfwPollEvents();
        // cout<<456<<endl;
        //选择清空的颜色RGBA
        glClearColor(0, 0, 0, 1);
        glClear(GL_COLOR_BUFFER_BIT);
        // glColor3f(0,0, 0);
        glMatrixMode(GL_PROJECTION);

        LineBres_1(Point(0,0),Point(100,70));
        LineBres_1(Point(0,0),Point(100,-70));
        LineBres_1(Point(0,0),Point(70,100));
        LineBres_1(Point(0,0),Point(-70,100));
        LineBres_1(Point(0,0),Point(-100,70));
        LineBres_1(Point(0,0),Point(-70,-100));
        LineBres_1(Point(0,0),Point(-100,-70));
        LineBres_1(Point(0,0),Point(70,-100));

        LineBres_1(Point(0,0),Point(0,100));
        LineBres_1(Point(0,0),Point(0,-100));
        LineBres_1(Point(0,0),Point(100,0));
        LineBres_1(Point(0,0),Point(-100,0));
        LineBres_1(Point(0,0),Point(0,0));



        /******交换缓冲区，更新window上的内容******/
        glfwSwapBuffers(window);
        //break;
    }
    glfwTerminate();
    return 0;
}

运行结果
运行结果846×884 46.7 KB

中点法推导直线(0＜m＜1)决策参数，并表示与Bresenham里的参数相同

中点法推导

定义F(x,y) = mx-y+b, m定义与上面相同

根据直线方程定义当F(x_k+1,y_k+\frac12)>0时，说明中点在线的上方，此时画(x_k+1,y_k), 否则画(x_k+1,y_k+1)

令决策参数p_k=2∆x*F(x_k+1, y_k+\frac{1}{2})(为什么要乘以2∆x, 我先用2∆x推导了一遍发现的)

=2∆x*(m*(x_k+1)-(y_k+\frac{1}{2})+b)

=2∆y*(x_k+1) -2∆x*y_k + ∆x*(2b-1)

p_{k+1}=2∆y*(x_k+1+1) -2∆x*y_{k+1} + ∆x*(2b-1)

p_{k+1} - p_k = 2∆y+\begin{cases}-2∆x, p_k<=0\\0, p_k>0\end{cases}

p_0=2∆y*(x_0+1) -2∆x*(m*x_0+b) + ∆x*(2b-1)=2∆y-∆x

可以看出p_k的增量是与Bresenham相同的。
这也解释了我当时的疑惑：为什么没有中点法画线

1 个赞