AK F.*ing leetcode 流浪计划之线段树

算法之美
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

@[toc]

零、简介

之前介绍过树状数组、前缀和、RMQ-ST算法（添加引用 ），这些都是区间求值的算法。

上述方法优点是代码实现简单，缺点是应用单一，有些场景就用不了。

今天介绍一个更高级的算法，可说是上述类似问题的大杀器，如果遇到区间问题，又解不了，这个算法有可能给出答案。

线段树算法有点类似于动态规划，事先把子问题的答案先计算出来并存储。在查询时，对区间进行二分，直到找到所有已经存储答案的区间并综合计算出结果。其空间复杂度是O(n), 每次更新或查询的时间复杂度是O(log(n))。

本文从朴素分组算法出发，引出动态规划方法，最后再优化空间复杂度引出RMQ-ST，图文结合，讲解原理。

一、算法原理

以下我们以动态区间求和为例，说明一下树的构建，更新，及查询过程。

原题链接 力扣

307. 区域和检索 - 数组可修改

树的构建

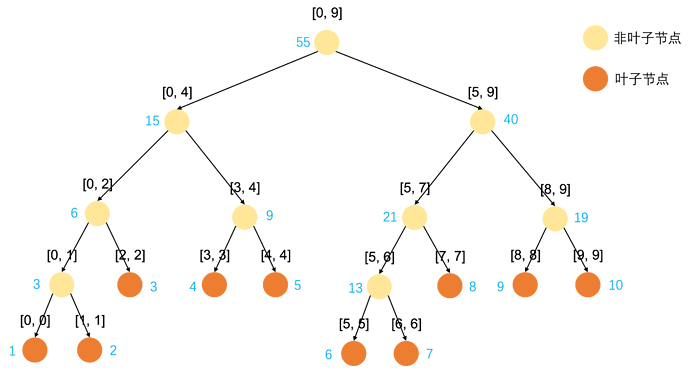
把一个区间看成一条线段，一开始整条线段是根结点，把线段分成2半，生成新的2条线段，做为其左右孩子。对左右孩子继续上面的操作，直到线段长度为1结束。

假设初始数组为arr=[1,2,3,4,5,6,7,8,9,10]

长度为10，则最大是区间[0，9]为例，构建树如下。

建树过程
建树过程4170×2245 283 KB

上图中黑色字为区间，蓝色字为区间和。

整个建树过程是一个深度优先遍历的过程。叶子节点的和就是原始值。

非叶子结点的和为左右孩子之和。

从上图中可以看出，整棵树是一棵平衡树，叶子结点个数是len(arr)个。

由于有些可能处于最后第二层。故总体结点个数有可能会超过2*len(arr), 但不是会超过4*len(arr), 时间复杂度为O(n)

更新

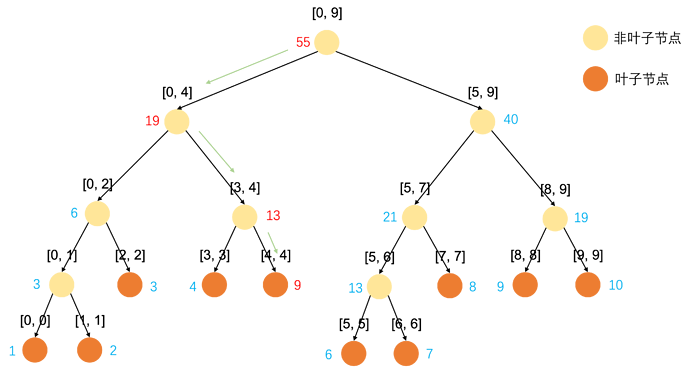
以更新arr[4]=9 为例。

先去找到区间[4,4]叶子结点，并更新为9，现更新父结点和为左右孩子之和。

更新值
更新值4170×2245 291 KB

查找过程：比较右左孩子的区间，判断4在哪个孩子区间中就往哪边走。

当遇到叶子节点时就更新其值，然后往回更新父结点的和。

由于每次区间都会减少一半，故时间复杂度为O(log(n))

查询

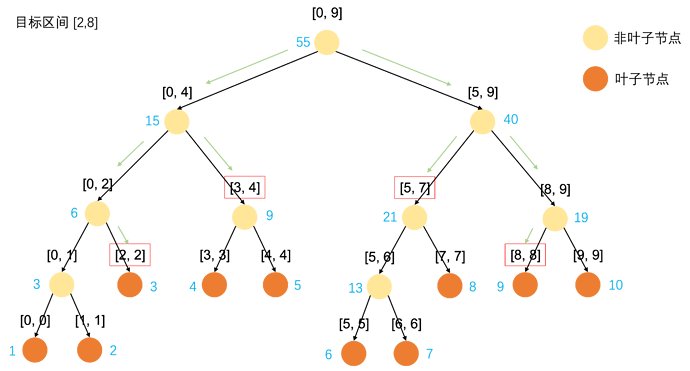
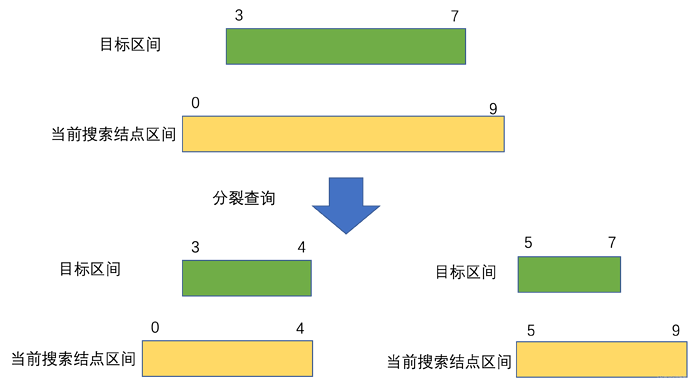
以查询区间[2, 8]为例。

遍历过程采用深度优先遍历加剪枝的方法进行。

如果父结点区间与查询区间没有交集则直接返回。

如果有交集则遍历左右孩子。

如果遇到当前区间被查询区间完全包含，则返回结果。

查询过程
查询过程4170×2245 329 KB

绿线为查询路径，红框为符合条件的区间所有红框中的结果相加即是区间[2，8]的和。

查询复杂度为O(log(n))。

二、数据结构及算法实现

数据结构

// 树结点定义
type node struct {
   l, r                  int // 代表树结点代表的区间范围
   leftChild, rightChild *node
   sum                   int // 区间总和
}

// 线段树定义
type SegmentTree struct {
   nodes []node // 事先申请结点，加事内存分配
   root  int    //根结点编号
}

构建

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
   tree.nodes = make([]node, (r-l+1)*4) // 要申请根结点的4倍
   tree.root = 1 //
   tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
   if l > r {
      return nil
   }

   mid := (l + r) >> 1
   tree.nodes[root].l, tree.nodes[root].r = l, r
   tree.nodes[root].sum = 0 //初始为0，查询前通过单点更新初始值
   if l == r {
      return &tree.nodes[root]
   }
   // 构造左右子树
   tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
   tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
   return &tree.nodes[root]
}

更新

func (tree *SegmentTree) UpdatePoint(x, val int) {
   tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
   if l > tree.nodes[root].r || r < tree.nodes[root].l { // 超出范围
      return
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      tree.nodes[root].sum = val
      return
   }

   tree.update(l, r, val, root<<1)
   tree.update(l, r, val, root<<1|1)

   // 更新完孩子，更新自己
   tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

查询

func (tree *SegmentTree) QueryRange(l, r int) int {
   return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
   if l > tree.nodes[root].r || r < tree.nodes[root].l { // 超出范围按0处理
      return 0
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r { // 被目标区间覆盖
      return tree.nodes[root].sum
   }

   return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1) // 查询左右子树
}

复杂度分析

建树与更新比较好理解，不再赘述。

主要看一下查询复杂度。

来分4种情况讨论：

  1. 当前区间被目标区间包含，直接返回O(1)
  2. 当前区间与目标区间没有交集，直接返回O(1)
  3. 当前区间包含目标区间且有一端重合。
  4. 当前区间包含目标区间且没有一端重合。

情况1，2好理解。

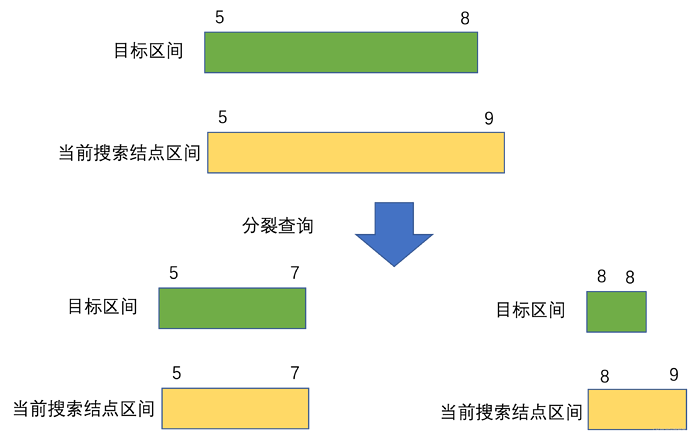
情况3如下图所示

一端重合分裂查询
一端重合分裂查询3167×1993 110 KB

从上图中可以看出，当有一端重合时，子查询中肯定有一个是满足条件1。另一个继续分裂，相当于每次把长度除以2, 根据二分法复杂度，O(log(n))。

情况4如下图：

两端不重合
两端不重合3607×1993 113 KB

情况4 可以分裂成2个情况3。总体复杂度也是O(log(n))。

所以查询的总体复杂度是O(log(n))。

例题题解

// 树结点定义
type node struct {
   l, r                  int // 代表树结点代表的区间范围
   leftChild, rightChild *node
   sum                   int // 区间总和
}

// 线段树定义
type SegmentTree struct {
   nodes []node // 事先申请结点，加事内存分配
   root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
   tree.nodes = make([]node, (r-l+1)*4)
   tree.root = 1 //
   tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
   if l > r {
      return nil
   }

   mid := (l + r) >> 1
   tree.nodes[root].l, tree.nodes[root].r = l, r
   tree.nodes[root].sum = 0
   if l == r {
      return &tree.nodes[root]
   }
   // 构造左右子树
   tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
   tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
   return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
   tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      tree.nodes[root].sum = val
      return
   }

   tree.update(l, r, val, root<<1)
   tree.update(l, r, val, root<<1|1)

   // 更新完孩子，更新自己
   tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

func (tree *SegmentTree) QueryRange(l, r int) int {
   return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return 0
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      return tree.nodes[root].sum
   }

   return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

type NumArray struct {
   tree *SegmentTree
}

func Constructor(nums []int) NumArray {
   na := NumArray{}
   na.tree = &SegmentTree{}
   na.tree.Init(0, len(nums))
   for i, v := range nums {
      na.Update(i, v)
   }

   return na
}

func (this *NumArray) Update(index int, val int) {
   this.tree.UpdatePoint(index, val)
}

func (this *NumArray) SumRange(left int, right int) int {
   return this.tree.QueryRange(left, right)
}

/**
 * Your NumArray object will be instantiated and called as such:
 * obj := Constructor(nums);
 * obj.Update(index,val);
 * param_2 := obj.SumRange(left,right);
 */

三、算法模板

// 树结点定义
type node struct {
   l, r                  int // 代表树结点代表的区间范围
   leftChild, rightChild *node
   sum                   int // 区间总和
}

// 线段树定义
type SegmentTree struct {
   nodes []node // 事先申请结点，加事内存分配
   root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
   tree.nodes = make([]node, (r-l+1)*4)
   tree.root = 1 //
   tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
   if l > r {
      return nil
   }

   mid := (l + r) >> 1
   tree.nodes[root].l, tree.nodes[root].r = l, r
   tree.nodes[root].sum = 0
   if l == r {
      return &tree.nodes[root]
   }
   // 构造左右子树
   tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
   tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
   return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
   tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      tree.nodes[root].sum = val
      return
   }

   tree.update(l, r, val, root<<1)
   tree.update(l, r, val, root<<1|1)

   // 更新完孩子，更新自己
   tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

func (tree *SegmentTree) QueryRange(l, r int) int {
   return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return 0
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      return tree.nodes[root].sum
   }

   return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

四、区间更新与优化

先来看下面这题

http://acm.hdu.edu.cn/showproblem.php?pid=1698

题目大意

一根金属链由N块金属块组成，金属各类有金银铜三种，价值分别为1，2，3.

问经过Q次操作后，整条链的价值总和是多少。

每次操作是选定一个区间，然后把这个区间的每块金属替换成某种金属。

0<=Q<=100,000

1<=N<=100,000

1<=X<=Y<=N, Z, 1<=Z<=3

题目分析

朴素做法

根据上题的做法，每次区间更新可以变成单值更新，代码如下

// 单次更新
func UpdateRange(st *SegmentTree, X, Y, Z int ) {
	for i:=X; i<=Y;i++ {
		st.UpdatePoint(i, Z)
	}
}

上述代码每次复杂度为O(Nlog(N)), 需要操作Q次操作 总复杂度为 O(QNlog(N)), 不满足题意。

优化

当某个树结点中所有金属相同时，可不需要下沉，只要记一下当前金属以及总长度即可计算出整体长度。

在结点中加入2个字段。

// 树结点定义
type node struct {
   l, r                  int // 代表树结点代表的区间范围
   leftChild, rightChild *node
   sum                   int // 区间总和
   lazyPrice						 int // >0 代表此区间被设置成某个值, sum = lazyPrice* (r-l+1);，=0 未设置，sum 取子节点之和。
}

更新逻辑

func (tree *SegmentTree) down(root int) {
	 if tree.nodes[root].lazyPrice==0 {
	 		return
	 }
	 lazyPrice := tree.nodes[root].lazyPrice
	 tree.nodes[root].lazyPrice = 0
	 // 传递给子结点
	 left := tree.nodes[root<<1]
	 tree.update(left.l, left.r, lazyPrice, root<<1)
	 right := tree.nodes[root<<1|1]
	 tree.update(right.l, right.r, lazyPrice, root<<1|1)
}

func (tree *SegmentTree) update(l, r, val, root int) {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      tree.nodes[root].sum = val * (tree.nodes[root].r-tree.nodes[root].l+1)
      tree.nodes[root].lazyPrice = val
      return
   }
	 // 如果之前设置过lazyPrice, 需要先分下去
	 tree.down(root)

   tree.update(l, r, val, root<<1)
   tree.update(l, r, val, root<<1|1)

   // 更新完孩子，更新自己
   tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

查询逻辑

func (tree *SegmentTree) query(l, r, root int) int {
   if l > tree.nodes[root].r || r < tree.nodes[root].l {
      return 0
   }

   if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
      return tree.nodes[root].sum
   }
   
   // 如果之前设置过lazyPrice, 需要先分下去
	 tree.down(root)

   return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

AC代码

C++

#include <iostream>
#include<vector>
#include<string>
#include<cstring>
#include<stdio.h>
#include<map>
#include<set>
#include<algorithm>

using namespace std;

#define lson(x) (x<<1)
#define rson(x) (x<<1|1)

const int M = 1e5+10;

class Node {
public:
    int left, right, mid;
    int sumVal;
    int lazyPrice;

    Node() {
    }
};

Node node[M*4];
class segmentTree {
private:
    void buildTree(int ind, int l, int r) {
        node[ind].left=l;
        node[ind].right=r;
        node[ind].sumVal = 0;
        node[ind].mid = l + r >> 1;
        if (l == r) {
            return;
        }

        buildTree(lson(ind), l, node[ind].mid);
        buildTree(rson(ind), node[ind].mid + 1, r);
    }


    void pushDown(int ind) {
        if (node[ind].lazyPrice == 0) return;

        this->updateTree(lson(ind), node[lson(ind)].left, node[lson(ind)].right, node[ind].lazyPrice);
        this->updateTree(rson(ind), node[rson(ind)].left, node[rson(ind)].right, node[ind].lazyPrice);
        node[ind].lazyPrice = 0;
    }

public:
    segmentTree(int left, int right) {
        buildTree(1, left, right);
    }

    void updateTree(int ind, int l, int r, int val) {
        if (l > node[ind].right || r < node[ind].left)return;

        if (l <= node[ind].left && node[ind].right <= r) {
            node[ind].sumVal = val * (node[ind].right - node[ind].left + 1);
            node[ind].lazyPrice = val;
            return;
        }

        pushDown(ind);

        updateTree(lson(ind), l, r, val);
        updateTree(rson(ind), l, r, val);

        node[ind].sumVal = node[lson(ind)].sumVal + node[rson(ind)].sumVal;
    }

    int query(int ind, int l, int r) {

        if (l > node[ind].right || r < node[ind].left)return 0;

        if (l <= node[ind].left && node[ind].right <= r) {
            return node[ind].sumVal;
        }

        pushDown(ind);
        return query(lson(ind), l, r) + query(rson(ind), l, r);
    }
};


int main() {
    int T, N, Q;
    cin >> T;
    for (int k = 1; k <= T; k++) {
        cin >> N >> Q;
        segmentTree seg = segmentTree(1, N);
        seg.updateTree(1, 1, N, 1);
        // cout << "lq1:" << seg.query(1, 1, N) << endl;
        while (Q--) {
            int x, y, z;
            scanf("%d%d%d", &x, &y, &z);
            // cout << x << "-" << y << "-" << z << endl;
            seg.updateTree(1, x, y, z);
            // cout << "lq:" << seg.query(1, 1, N) << endl;
        }

        printf("Case %d: The total value of the hook is %d.\n", k, seg.query(1, 1, N));
    }

    return 0;
}

/*
2
10
2
1 5 2
5 9 3
10
2
1 5 2
5 9 3
*/

go

package main

import "fmt"

// 树结点定义
type node struct {
	l, r                  int // 代表树结点代表的区间范围
	leftChild, rightChild *node
	sum                   int // 区间总和
	lazyPrice             int // >0 代表此区间被设置成某个值, sum = lazyPrice* (r-l+1);，=0 未设置，sum 取子节点之和。
}

// 线段树定义
type SegmentTree struct {
	nodes []node // 事先申请结点，加事内存分配
	root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
	tree.nodes = make([]node, (r-l+1)*4)
	tree.root = 1 //
	tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
	if l > r {
		return nil
	}

	mid := (l + r) >> 1
	tree.nodes[root].l, tree.nodes[root].r = l, r
	tree.nodes[root].sum = 0
	if l == r {
		return &tree.nodes[root]
	}
	// 构造左右子树
	tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
	tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
	return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
	tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) UpdateRange(x, y, val int) {
	tree.update(x, y, val, tree.root)
}

func (tree *SegmentTree) down(root int) {
	if tree.nodes[root].lazyPrice == 0 {
		return
	}
	lazyPrice := tree.nodes[root].lazyPrice
	tree.nodes[root].lazyPrice = 0
	// 传递给子结点
	left := tree.nodes[root<<1]
	tree.update(left.l, left.r, lazyPrice, root<<1)
	right := tree.nodes[root<<1|1]
	tree.update(right.l, right.r, lazyPrice, root<<1|1)
}

func (tree *SegmentTree) update(l, r, val, root int) {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		tree.nodes[root].sum = val * (tree.nodes[root].r - tree.nodes[root].l + 1)
		tree.nodes[root].lazyPrice = val
		return
	}
	// 如果之前设置过lazyPrice, 需要先分下去
	tree.down(root)

	tree.update(l, r, val, root<<1)
	tree.update(l, r, val, root<<1|1)

	// 更新完孩子，更新自己
	tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

func (tree *SegmentTree) QueryRange(l, r int) int {
	return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return 0
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		return tree.nodes[root].sum
	}

	// 如果之前设置过lazyPrice, 需要先分下去
	tree.down(root)

	return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

func main() {
	var T, N, Q int

	fmt.Scanf("%d", &T)
	for k:=1; k<=T; k++ {
		fmt.Scanf("%d\n%d", &N, &Q)
		tree := &SegmentTree{}
		tree.Init(1, N)
		tree.UpdateRange(1,N, 1) // 默认1
		for i := 0; i < Q; i++ {
			var x, y, z int
			fmt.Scanf("%d%d%d", &x, &y, &z)
			tree.UpdateRange(x, y, z)
			// fmt.Println("ql:",tree.QueryRange(1, N))
		}
		//Case 1: The total value of the hook is 24.
		fmt.Printf("Case %d: The total value of the hook is %d.", k , tree.QueryRange(1, N))
	}
}

/*

2
10
2
1 5 2
5 9 3
10
2
1 5 2
5 9 3

 */

五、牛刀小试

练习1 重做例题

区域和检索 - 数组可修改

https://leetcode-cn.com/problems/range-sum-query-mutable/

题目大意

略

题目解析

直接利用模板

AC代码

// 树结点定义
type node struct {
	l, r                  int // 代表树结点代表的区间范围
	leftChild, rightChild *node
	sum                   int // 区间总和
}

// 线段树定义
type SegmentTree struct {
	nodes []node // 事先申请结点，加事内存分配
	root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
	tree.nodes = make([]node, (r-l+1)*4)
	tree.root = 1 //
	tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
	if l > r {
		return nil
	}

	mid := (l + r) >> 1
	tree.nodes[root].l, tree.nodes[root].r = l, r
	tree.nodes[root].sum = 0
	if l == r {
		return &tree.nodes[root]
	}
	// 构造左右子树
	tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
	tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
	return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
	tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		tree.nodes[root].sum = val
		return
	}

	tree.update(l, r, val, root<<1)
	tree.update(l, r, val, root<<1|1)

	// 更新完孩子，更新自己
	tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

func (tree *SegmentTree) QueryRange(l, r int) int {
	return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return 0
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		return tree.nodes[root].sum
	}

	return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

type NumArray struct {
	tree *SegmentTree
}

func Constructor(nums []int) NumArray {
	na := NumArray{}
	na.tree = &SegmentTree{}
	na.tree.Init(0, len(nums))
	for i, v := range nums {
		na.Update(i, v)
	}

	return na
}

func (this *NumArray) Update(index int, val int) {
	this.tree.UpdatePoint(index, val)
}

func (this *NumArray) SumRange(left int, right int) int {
	return this.tree.QueryRange(left, right)
}

/**
 * Your NumArray object will be instantiated and called as such:
 * obj := Constructor(nums);
 * obj.Update(index,val);
 * param_2 := obj.SumRange(left,right);
 */

练习2 结合离散化扫描图形

题目链接：力扣

题目大意

城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],…] ，并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[…[2 3], [4 5], [12 7], …]

示例 1：

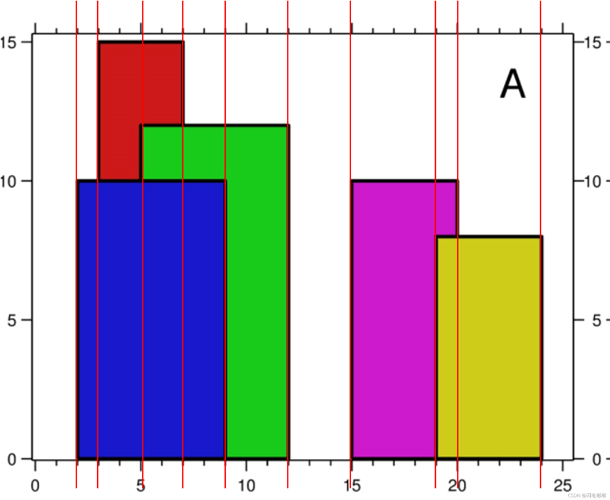
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
示例 2：

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

提示：

1 <= buildings.length <= 10^4
0 <= lefti < righti <= 2^31 - 1
1 <= heighti <= 2^31 - 1
buildings 按 lefti 非递减排序

题目解析

点出现的位置
点出现的位置2438×1998 271 KB

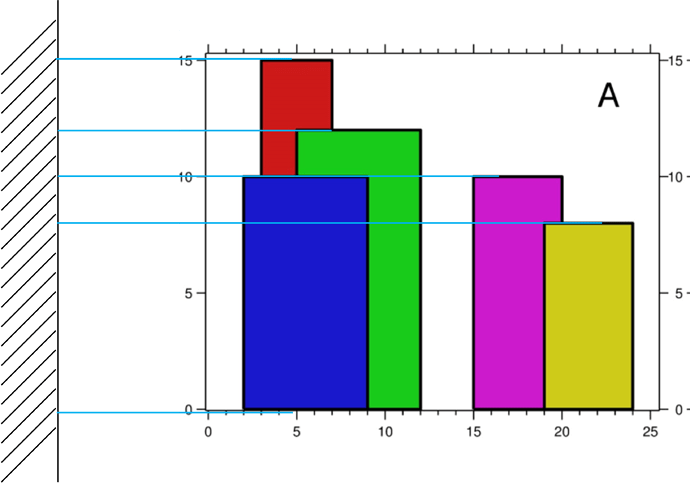
通过分析可以得出关键点肯定是出现在矩形的左右边上，且边的最上边点是关键点，即图中的红色位置。

我们称关键点所在的边为关键边。

那么对于一边如何判断其是否可以成关键边。

直观的方法就是看这条边是不是完全被其他图形覆盖。

可以利用图像扫描法进行判断。

映射
映射3290×2305 332 KB

我们从左到右遍历矩形的边，

当遇到一个矩形左边时，先查询有没有比自身高的线已经映射，如果没有就是关键边，然后把它映射到墙上。

当遇到右边时，先从墙上删除，再查询目前墙上最高高度是不是低于自身。

比如高度为5，只要查询在此之前y大等5的线段有没有即可。用线段树可实现区间查询。

优化点：

  1. 事先对边进行排序，按x从小到大排序，同一x坐标，添加操作排前面，如果同为添加高度高的排在前面，否则高的排后面。
  2. 离散化数据，由于高度最高2^31 - 1，线段区间不能开到[0，2^31 - 1]。因为 buildings.length <= 10^4，最多只要10^4个数字来表示长度。

AC代码

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

// 树结点定义
type node struct {
	l, r                  int // 代表树结点代表的区间范围
	leftChild, rightChild *node
	maxVal                int // 区间最大
	cnt                   int
}

// 线段树定义
type SegmentTree struct {
	nodes []node // 事先申请结点，加事内存分配
	root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
	tree.nodes = make([]node, (r-l+1)*4)
	tree.root = 1 //
	tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
	if l > r {
		return nil
	}

	mid := (l + r) >> 1
	tree.nodes[root].l, tree.nodes[root].r = l, r
	tree.nodes[root].maxVal = 0
	tree.nodes[root].cnt = 0
	if l == r {
		return &tree.nodes[root]
	}
	// 构造左右子树
	tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
	tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
	return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
	tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r { // 单点更新，肯定是页子结点
		tree.nodes[root].cnt += val
		if tree.nodes[root].cnt <= 0 {
			tree.nodes[root].maxVal = 0
		} else {
			tree.nodes[root].maxVal = tree.nodes[root].r
		}
		return
	}

	tree.update(l, r, val, root<<1)
	tree.update(l, r, val, root<<1|1)

	// 更新完孩子，更新自己
	tree.nodes[root].maxVal = max(tree.nodes[root<<1].maxVal, tree.nodes[root<<1|1].maxVal)
}

func (tree *SegmentTree) QueryRange(l, r int) int {
	return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return 0
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		return tree.nodes[root].maxVal
	}

	return max(tree.query(l, r, root<<1), tree.query(l, r, root<<1|1))
}

// 离散化模板
func getInd(buildings [][]int) ([]int, map[int]int) {
	numMap := map[int]bool{0: true}

	for _, b := range buildings {
		numMap[b[2]] = true
	}

	nums := []int{}
	for k := range numMap {
		nums = append(nums, k)
	}

	sort.Ints(nums)
	index := map[int]int{}
	for i, n := range nums {
		index[n] = i
	}

	return nums, index
}

type Operations [][]int

func (x Operations) Len() int { return len(x) }
func (x Operations) Less(i, j int) bool {
	// x轴小优先
	if x[i][0] != x[j][0] {
		return x[i][0] < x[j][0]
	}

	// 添加操作优先
	if x[i][2] != x[j][2] {
		return x[i][2] > x[j][2]
	}

	// +时，y轴大优先
	if x[i][2] == 1 {
		return x[i][1] > x[j][1]
	}

	// - 时，y轴小优先
	return x[i][1] < x[j][1]
}

func (x Operations) Swap(i, j int) { x[i], x[j] = x[j], x[i] }

func getSkyline(buildings [][]int) [][]int {
	nums, index := getInd(buildings)
	op := [][]int{}
	for _, b := range buildings {
		op = append(op, []int{b[0], b[2], 1}, []int{b[1], b[2], -1})
	}
	sort.Sort(Operations(op))

	tree := &SegmentTree{}
	tree.Init(0, len(index))

	ans := [][]int{}

	for _, o := range op {
		h1 := tree.QueryRange(0, len(index))
		tree.UpdatePoint(index[o[1]], o[2])
		if o[2] == 1 {
			if nums[h1] < o[1] {
				ans = append(ans, []int{o[0], o[1]})
			}
		} else {
			h2 := tree.QueryRange(0, len(index))
			if nums[h2] < o[1] {
				ans = append(ans, []int{o[0], nums[h2]})
			}
		}
	}

	return ans
}
/*
fmt.Printf("%+v\n", getSkyline([][]int{{1, 2, 3}, {1, 2, 3}, {1, 2, 3}, {2,4,3}}))
	fmt.Printf("%+v\n", getSkyline([][]int{{1, 2, 3}, {1, 2, 3}, {1, 2, 3}, {2,4,5}}))
	fmt.Printf("%+v\n", getSkyline([][]int{{1, 2, 3}, {1, 2, 3}, {1, 2, 3}, {12,14,5}}))
	*/

练习3 区间计数

题目链接：力扣

题目大意

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。

你需要返回给定数组中的重要翻转对的数量。

示例 1:

输入: [1,3,2,3,1]
输出: 2
示例 2:

输入: [2,4,3,5,1]
输出: 3
注意:

给定数组的长度不会超过50000。
输入数组中的所有数字都在32位整数的表示范围内。

题目解析

从前往后遍历依次加入到线段树中，对于每个nums[i], 查询 2*nums[i]+1 到最大值的个数。

由于数据范围较大，也需要做离散化处理。

AC代码

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

// 树结点定义
type node struct {
	l, r                  int // 代表树结点代表的区间范围
	leftChild, rightChild *node
	sum                   int // 区间和
}

// 线段树定义
type SegmentTree struct {
	nodes []node // 事先申请结点，加事内存分配
	root  int    //根结点编号
}

// 初始化线段树，分配内存大小, 构造树型
func (tree *SegmentTree) Init(l, r int) {
	tree.nodes = make([]node, (r-l+1)*4)
	tree.root = 1 //
	tree.buildNode(l, r, tree.root)
}

// 构造树型
func (tree *SegmentTree) buildNode(l, r, root int) *node {
	if l > r {
		return nil
	}

	mid := (l + r) >> 1
	tree.nodes[root].l, tree.nodes[root].r = l, r
	tree.nodes[root].sum = 0
	if l == r {
		return &tree.nodes[root]
	}
	// 构造左右子树
	tree.nodes[root].leftChild = tree.buildNode(l, mid, root<<1)
	tree.nodes[root].rightChild = tree.buildNode(mid+1, r, root<<1|1)
	return &tree.nodes[root]
}

func (tree *SegmentTree) UpdatePoint(x, val int) {
	tree.update(x, x, val, tree.root)
}

func (tree *SegmentTree) update(l, r, val, root int) {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r { // 单点更新，肯定是页子结点
		tree.nodes[root].sum += val
		return
	}

	tree.update(l, r, val, root<<1)
	tree.update(l, r, val, root<<1|1)

	// 更新完孩子，更新自己
	tree.nodes[root].sum = tree.nodes[root<<1].sum + tree.nodes[root<<1|1].sum
}

func (tree *SegmentTree) QueryRange(l, r int) int {
	return tree.query(l, r, tree.root)
}

func (tree *SegmentTree) query(l, r, root int) int {
	if l > tree.nodes[root].r || r < tree.nodes[root].l {
		return 0
	}

	if l <= tree.nodes[root].l && tree.nodes[root].r <= r {
		return tree.nodes[root].sum
	}

	return tree.query(l, r, root<<1) + tree.query(l, r, root<<1|1)
}

// 离散化模板
func getInd(nums []int) ([]int, map[int]int) {
	numMap := map[int]bool{0: true}

	for _, n := range nums {
		numMap[n] = true
		numMap[2*n+1] = true // 方便查询把2*n+1也离散化
	}

	list := []int{}
	for k := range numMap {
		list = append(list, k)
	}

	sort.Ints(list)
	index := map[int]int{}
	for i, n := range list {
		index[n] = i
	}

	return list, index
}

func reversePairs(nums []int) int {
	_, index := getInd(nums)
	tree := &SegmentTree{}
	tree.Init(0, len(index))

	ans :=0
	for _, n:= range nums {
		ans +=tree.QueryRange(index[n*2+1], len(index))
		tree.UpdatePoint(index[n], 1)
	}

	return ans
}

五、总结

主要内容：

  1. 本文详细介绍了线段树原理，以及在区间更新时的优化，并对其复杂度进行分析和解释。

  2. 作用：基本上所有动态区间操作与查询都可以实现，包括以前的求和，求最值，区间覆盖等。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

六、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动手把刚才的题A了。

  1. 区域和检索 - 数组可修改：力扣
  2. 动态区间更新与求和：Problem - 1698
  3. 结合离散化扫描图形：力扣
  4. 区间计数：力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

  1. 力扣

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

hdu

以下将序号替换就是题目链接。

  1. Problem - 1166
  2. Problem - 1754
  3. Problem - 1698
  4. Problem - 2795
  5. Problem - 1540
  6. Problem - 1542
  7. Problem - 1255
  8. Problem - 1828
  9. http://acm.hdu.edu.cn/showproblem.php?pid=3308
  10. http://acm.hdu.edu.cn/showproblem.php?pid=3577
  11. Problem - 3486
  12. http://acm.hdu.edu.cn/showproblem.php?pid=3397
  13. http://acm.hdu.edu.cn/showproblem.php?pid=1823

Poj

以下将序号替换就是题目链接。

  1. 2777 -- Count Color
  2. 3468 -- A Simple Problem with Integers
  3. 2528 -- Mayor's posters
  4. 3667 -- Hotel

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。

在这里插入图片描述