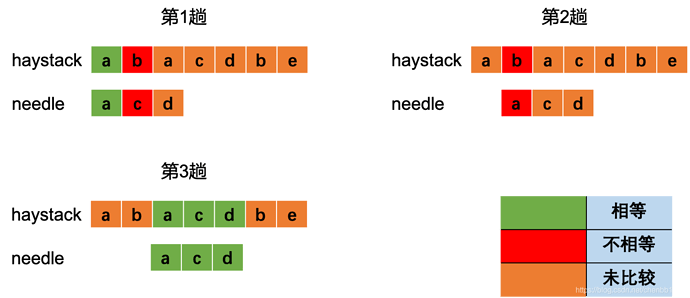AK F.*ing leetcode 流浪计划之KMP

算法之美
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

零、简介

KMP算法是一个让人听到就害怕的算法，原因在于其原理比较难理解。看好几遍也看不懂。往往遇到字符匹配问题就绕不开。其主要作用有：字符串匹配，计算字符串循环周期，根据next定义也可以求解字符串最长公共后缀前缀。

本文从朴素匹配算法出发，优化移动次数，图文结合，证明其实定理的正确性，全面理解KMP。

KMP算法主要包括next数组计算，以及串匹配2个过程，其中next数组本身可以计算字符串循环周期的作用。

为了方便说明，以下作了一些符号定义

s为非空字符串

  • s[i,j] 为s从第i个字符到第j个字符组成的子串
  • s[0,i] 为以第i个字符结尾的s前缀
  • s[i,len(s)-1]为以第i个字符开始的的s后缀

一、字符串匹配从朴素思想到KMP

基本问题

https://leetcode-cn.com/problems/implement-strstr/

实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

示例 1：

输入：haystack = “hello”, needle = “ll”
输出：2
示例 2：

输入：haystack = “aaaaa”, needle = “bba”
输出：-1
示例 3：

输入：haystack = “”, needle = “”
输出：0

  • 0 <= haystack.length, needle.length <= 5 * 104
  • haystack 和 needle 仅由小写英文字符组成

朴素思想（逐个后移法）

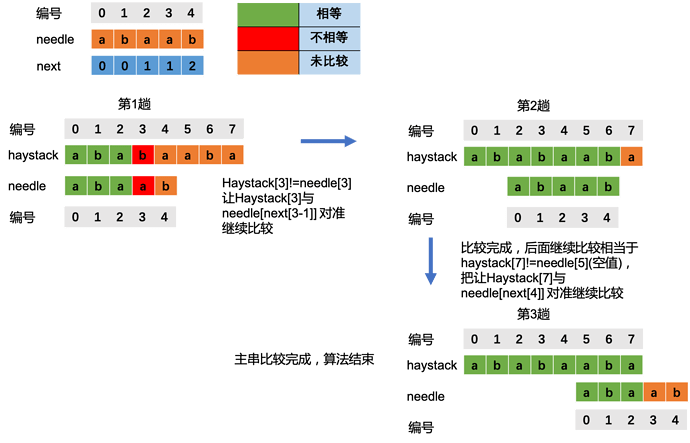
从前往后依次选择haystack[i] 为开头与needle进行比较，如果成功就返回，不成功就把i后移。

1472×637 43.5 KB

上图中每次比较到不相等时就后移，当比较到第3趟时发现了完整匹配。

/*
从前往后依次选择haystack[i] 为开头与needle进行比较，如果成功就返回，
不成功就把i后移。
*/
func strStr(haystack string, needle string) int {
	if needle == "" {
		return 0
	}
	for i := 0; i < len(haystack); i++ {
		j := 0
		// 以haystack[i]开始比较
		for ; j < len(needle) && i+j < len(haystack); j++ {
			if haystack[i+j] != needle[j] {
				break
			}
		}
		if j == len(needle) {
			return i
		} // 成功直接返回，不成功i 后移
	}

	return -1
}

上述算法每一趟的极端情况要比较len(needle)次。所以，总体复杂度是len(needle)*len(haystack)。

引出优化算法（KMP）

上述算法是每次到匹配不上时往后移一个（这里转变一下，将needle后移，效果其实一样），其实很多情况下第1个就匹配不上，所以是不是可以多移几个。这就意味着，移动之后至少有1个是匹配上的。那么怎么决定移几个呢。移多了怕错过前面的可行解，移少了效率不够高。这里KMP思想多加了一个条件，就是needle往后移时，要匹配上之前比较过的haystack的某个后缀。

根据贪心原理这个后缀当越长越好，越长意味着后移得越少，不会错过可行解。

1766×1218 129 KB

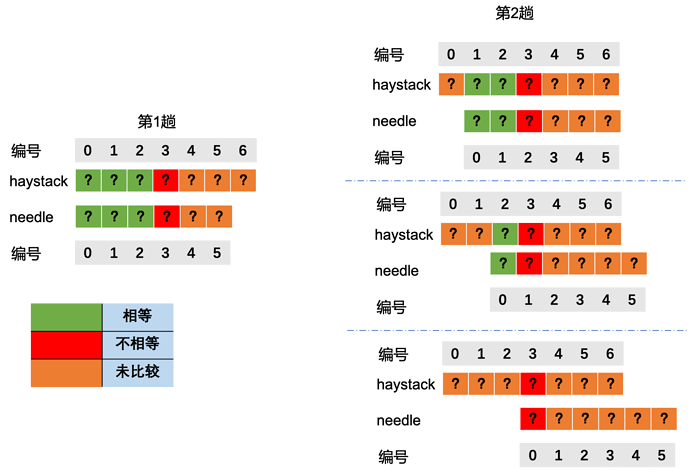
假如第1趟比较第needle[3]就不相等了，就有可能出现3种情况，needle后移1个，2个，3个，但不管怎么样，haystack已经比较过的是不会再比较了。

如何确定后移几个呢，KMP引入了一个next数组的概念。通过next数组可以快速O(1)确定后移几个。在下一部分会详细介绍。

后面继续比较，当发现不相等时又会将needle按照上述方法后移，直到比较完所有haystack字符。

从上述描述中可以看出当前比较的字符haystack[i] 是一直后移的，这个过程的复杂度是O(len(haystack))。后续会介绍next数组计算，其复杂度为O(len(needle)), 总复杂度为 O(len(haystack))+O(len(needle))。

二、NEXT数组详解

next数组定义

每个字符串都有自己的next数组，对于字符串s, 其next数组长度为len(s)的int数组。

其中next[i]的值定义如下：

设next[i] = k，则k的值是子串s0s1s2…si 最长公共前缀后缀长度（k<=i, 前缀和后缀不可以是子串本身）

看图，

908×927 55.9 KB

next数组在子串查找中的作用以及其正确性

回到上面的问题当失配以后要如何移动。

1197×902 48.5 KB

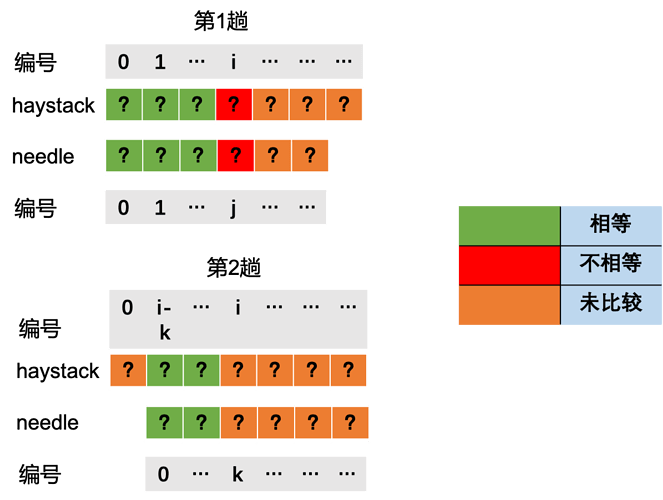
在上图中，当匹配到i时，字符失配了，这里首先有一个重要信息，haystack[0,i-1] = needle[0,j-1]， 这个结论很重要, 是后面结论的基石。

1304×954 65.1 KB

那么如果我们想要第2趟从needle的第k（k<j）个字符开始匹配, 则要满足haystack[i-k,i-1] = needle[0,k-1].

上图中蓝色框中的子串都是相同的。

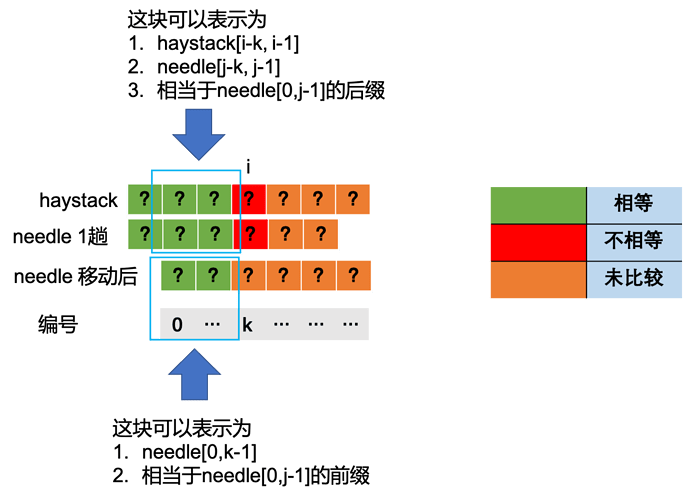
根据上述结论，haystack[0,i-1] = needle[0,j-1]，可以导出haystack[i-k,i-1] = needle[j-k, j-1]。

所以，haystack[i-k,i-1] = needle[0,k-1]该条件可以转变成 满足 needle[j-k, j-1] = needle[0,k-1]。根据贪心原理k越大越好。从图中可以看出这个K就是上面提到的next[j-1], 就是子串needle[0,j-1] 最长公共前缀后缀的长度。

由上述分析得出结论，当haystack[i]=needle[j]时 i++, j++, 否则 i不变，j=next[j-1](j>0)。

以下给出KMP算法(假设next已经计算出来了，可以先根据定义手动算一下，后面讲解next数组求解方法)

ype KMP struct {
	next    []int
	needle string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(needle string) []int {
	// todo
}

func (k *KMP) find(haystack string) []int {
	j := 0
	res := []int{}
	for i, c := range haystack {
		for j > 0 && c != int32(k.needle[j]) { //不相等就把模式串往后移，直到相等或从头开始
			j = k.next[j-1]
		}
		if c == int32(k.needle[j]) {// 比较下一个
			j++
		}
		if j == len(k.needle) { // 完全找到模式串
			res = append(res, i-len(k.needle)+1)// 添加结果
			j = k.next[j-1] // 查询下一处
		}
	}

	return res
}

图解如下：

2054×1320 176 KB

至此我们已经大概了解了KMP的基本思想及其主要工作原理。

下面有几个疑问要解释一下。

  1. 为什么每次失配后是移动到next[j-1]继续匹配

答：根据next[j-1]的定义，是needle[0,j-1]最长公共前缀后缀的长度。可以得到 haystack[i-next[j-1],i-1] = needle[0, next[j-1]] ，刚好继续比较，上图已经解释。

  1. 会不会移动太多导致错过可行解。

答：不会，next[j-1]已经是最大值了，i-next[j-1]是最小的，所以移动的是最小个数使得needle与haystack有部分可以匹配。

next数组求解方法

还是从next定义出发。

对于字符串s, 其next数组长度为len(s)的int数组。

其中next[i]的值定义如下：

设next[i] = k，则k的值是子串s[0,i]最长公共前缀后缀长度（k<=i, 前缀和后缀不可以是子串本身）

显然，next[0]=0。

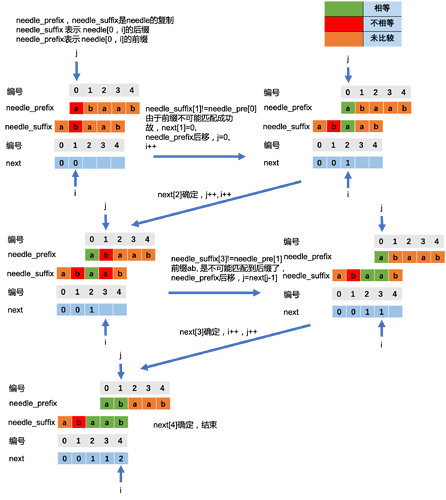
当 next[i]已经求出，求解next[i+1]时，根据定义可知s[0, next[i]-1] = s[i-next[i]+1,i]

如果 s[i+1] = s[next[i]] , 则 next[i+1] = next[i]+1，否则就要缩短目前已经匹配上的前缀和后缀，过程与上方needle往后移动类似。即下图中j=next[j-1] (j>0时，否则 j=0) 直到needle_prefix[j]==needle_suffix[i]。

这个过程要多看几遍，结合代码和看图。

2120×2375 276 KB

实际实现过程中并不需要复制needle, 只要用下标i,j 表示即可。

// 代码实现

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(needle string) []int {
	k.pattern = needle
	k.next = make([]int, len(needle))

	for i, j := 1, 0; i < len(needle); i++ {
		for j > 0 && needle[j] != needle[i] { // 这里一定要循环，举例 aaab
			j = k.next[j-1]
		}

		if needle[j] == needle[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

利用KMP算法求解

回过头来把一开始的题目使用KMP求解

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(pattern string) []int {
	k.pattern = pattern
	k.next = make([]int, len(pattern))

	for i, j := 1, 0; i < len(pattern); i++ {
		for j > 0 && pattern[j] != pattern[i] { // 这里一定要循环，举例 aaab
			j = k.next[j-1]
		}

		if pattern[j] == pattern[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

func (k *KMP) find(s string) []int {
	j := 0
	res := []int{}
	for i, c := range s {
		for j > 0 && c != int32(k.pattern[j]) { // 不相等就把模式串往后移，直到相等或从头开始
			j = k.next[j-1]
		}
		if c == int32(k.pattern[j]) { // 比较下一个
			j++
		}
		if j == len(k.pattern) {  // 完全找到模式串
			res = append(res, i-len(k.pattern)+1) // 添加结果
			j = k.next[j-1]  // 查询下一处
		}
	}

	return res
}

func strStr(haystack string, needle string) int {
	if needle == "" {
		return 0
	}
	kmp := &KMP{}
	kmp.makeNext(needle)
	ind := kmp.find(haystack)
	if len(ind) ==0 {return -1}
	return ind[0]
}
/*
"hello"
"ll"
"aaaaa"
"bba"
""
""
"aaaa"
"aaaa"
*/

三、KMP推论及证明

  • s的前缀后缀数组为next, 如果 len(s)%(len(s)-next[len(s)-1])==0（len(s)-next[len(s)-1]>0）, 则s可以由s[0,len(s)-next[len(s)-1]-1]循环得到，且s[0,len(s)-next[len(s)-1]-1]是s的最小循环。

证明：

1679×906 45.3 KB

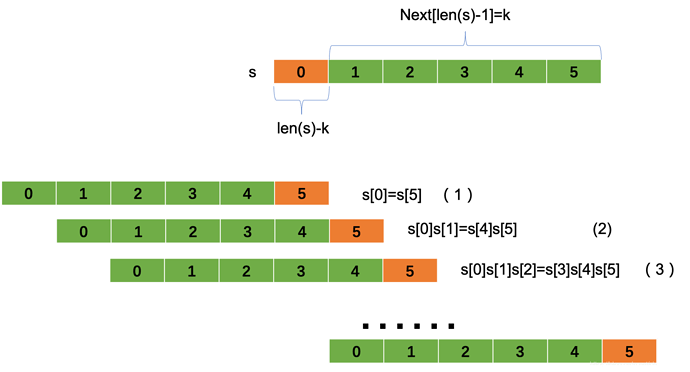
根据整除条件可知，可以将字符串分成若干等长的段。

图中分成了6段。根据next性质可以前5段和后缀5段整体是相等的。

那也不难得出图中1，2，3等式。

由1，2式可知s[0]=s[5]=s[1]=s[4]。同理可以推导出其他几段也是相等的。

故原命题得证。

怎么保证是最小循环节？反证法，如果不是最小，那么next[len(s)-1]必然有更大的值，而根据next定义已经是最大了。

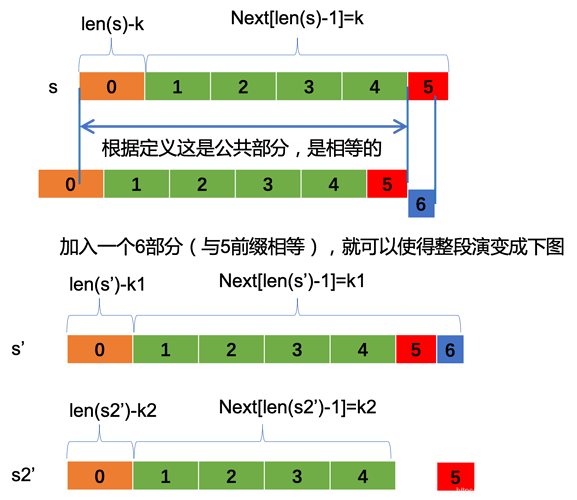
  • s的前缀后缀数组为next, 如果 len(s)(len(s)-next[len(s)-1])!=0, 由只需要在后面补充上 len(s)-next[len(s)-1] - len(s)(len(s)-next[len(s)-1])， 或最后面减掉len(s)%(len(s)-next[len(s)-1])个字符就可以使其循环(减掉有可能不会循环比如 abca).

证明：

1166×1010 67.5 KB

通过补齐，最终len(s’)%(len(s’) - next[len(s’)-1)=0。

通过删除，s2’也达到了循环。

四、算法模板

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(pattern string) []int {
	k.pattern = pattern
	k.next = make([]int, len(pattern))

	for i, j := 1, 0; i < len(pattern); i++ {
		for j > 0 && pattern[j] != pattern[i] {
			j = k.next[j-1]
		}

		if pattern[j] == pattern[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

func (k *KMP) find(s string) []int {
	j := 0
	res := []int{}
	for i, c := range s {
		for j > 0 && c != int32(k.pattern[j]) {
			j = k.next[j-1]
		}
		if c == int32(k.pattern[j]) {
			j++
		}
		if j == len(k.pattern) {
			res = append(res, i-len(k.pattern)+1)
			j = k.next[j-1] //查询可重叠
      // 查询不重叠 
      // j=0 重新开始
		}
	}

	return res
}

func (k *KMP) isRepeat() bool {
	if k.pattern=="" {
		return false
	}
	// 要先生成next数组
	l := len(k.pattern)
	if k.next[len(k.pattern)-1] == 0 {
		return false
	}

	return l%(l-k.next[l-1]) == 0
}

五、牛刀小试

练习1 子串查找

链接：力扣

回到刚开始的题目

题目大意

略

题目解析

先生成next数组，再查询即可。

AC代码

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(pattern string) []int {
	k.pattern = pattern
	k.next = make([]int, len(pattern))

	for i, j := 1, 0; i < len(pattern); i++ {
		for j > 0 && pattern[j] != pattern[i] { // 这里一定要循环，举例 aaab
			j = k.next[j-1]
		}

		if pattern[j] == pattern[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

func (k *KMP) find(s string) []int {
	j := 0
	res := []int{}
	for i, c := range s {
		for j > 0 && c != int32(k.pattern[j]) { // 不相等就把模式串往后移，直到相等或从头开始
			j = k.next[j-1]
		}
		if c == int32(k.pattern[j]) { // 比较下一个
			j++
		}
		if j == len(k.pattern) {  // 完全找到模式串
			res = append(res, i-len(k.pattern)+1) // 添加结果
			j = k.next[j-1]  // 查询下一处
		}
	}

	return res
}

func strStr(haystack string, needle string) int {
	if needle == "" {
		return 0
	}
	kmp := &KMP{}
	kmp.makeNext(needle)
	ind := kmp.find(haystack)
	if len(ind) ==0 {return -1}
	return ind[0]
}
/*
"hello"
"ll"
"aaaaa"
"bba"
""
""
"aaaa"
"aaaa"
*/

练习2 利用next数组查询最长公共前缀后缀

题目链接：力扣

题目大意

「快乐前缀」是在原字符串中既是 非空 前缀也是后缀（不包括原字符串自身）的字符串。

给你一个字符串 s，请你返回它的 最长快乐前缀。

如果不存在满足题意的前缀，则返回一个空字符串。

示例 1：

输入：s = “level”
输出：“l”
解释：不包括 s 自己，一共有 4 个前缀（“l”, “le”, “lev”, “leve”）和 4 个后缀（“l”, “el”, “vel”, “evel”）。最长的既是前缀也是后缀的字符串是 “l” 。
示例 2：

输入：s = “ababab”
输出：“abab”
解释：“abab” 是最长的既是前缀也是后缀的字符串。题目允许前后缀在原字符串中重叠。
示例 3：

输入：s = “leetcodeleet”
输出：“leet”
示例 4：

输入：s = “a”
输出：""

提示：

1 <= s.length <= 10^5
s 只含有小写英文字母

题目解析

利用next数组性质即可

AC代码

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(pattern string) []int {
	k.pattern = pattern
	k.next = make([]int, len(pattern))

	for i, j := 1, 0; i < len(pattern); i++ {
		for j > 0 && pattern[j] != pattern[i] {
			j = k.next[j-1]
		}

		if pattern[j] == pattern[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

func (k *KMP) find(s string) []int {
	j := 0
	res := []int{}
	for i, c := range s {
		for j > 0 && c != int32(k.pattern[j]) {
			j = k.next[j-1]
		}
		if c == int32(k.pattern[j]) {
			j++
		}
		if j == len(k.pattern) {
			res = append(res, i-len(k.pattern)+1)
			j = k.next[j-1]
		}
	}

	return res
}

func (k *KMP) isRepeat() bool {
	// 要先生成next数组
	if k.next[len(k.pattern)] == 0 {
		return false
	}
	l := len(k.pattern)

	return l%(l-k.next[l-1]) == 0
}


func longestPrefix(s string) string {
	if s == "" {
		return s
	}
	kmp := &KMP{}
	kmp.makeNext(s)
	return s[:kmp.next[len(s)-1]]
}

练习3 查询子串应用

题目链接：力扣

题目大意

给你两个字符串 s 和 part ，请你对 s 反复执行以下操作直到 所有 子字符串 part 都被删除：

找到 s 中 最左边 的子字符串 part ，并将它从 s 中删除。
请你返回从 s 中删除所有 part 子字符串以后得到的剩余字符串。

一个 子字符串 是一个字符串中连续的字符序列。

示例 1：

输入：s = “daabcbaabcbc”, part = “abc”
输出：“dab”
解释：以下操作按顺序执行：

  • s = “daabcbaabcbc” ，删除下标从 2 开始的 “abc” ，得到 s = “dabaabcbc” 。
  • s = “dabaabcbc” ，删除下标从 4 开始的 “abc” ，得到 s = “dababc” 。
  • s = “dababc” ，删除下标从 3 开始的 “abc” ，得到 s = “dab” 。
    此时 s 中不再含有子字符串 “abc” 。
    示例 2：

输入：s = “axxxxyyyyb”, part = “xy”
输出：“ab”
解释：以下操作按顺序执行：

  • s = “axxxxyyyyb” ，删除下标从 4 开始的 “xy” ，得到 s = “axxxyyyb” 。
  • s = “axxxyyyb” ，删除下标从 3 开始的 “xy” ，得到 s = “axxyyb” 。
  • s = “axxyyb” ，删除下标从 2 开始的 “xy” ，得到 s = “axyb” 。
  • s = “axyb” ，删除下标从 1 开始的 “xy” ，得到 s = “ab” 。
    此时 s 中不再含有子字符串 “xy” 。

提示：

1 <= s.length <= 1000
1 <= part.length <= 1000
s 和 part 只包小写英文字母。

题目解析

思路比较暴力，不停地查询子串删除即可，复杂度O(n^2)

AC代码

type KMP struct {
	next    []int
	pattern string
}

// a b a c a b a
// 0 0 1 0 1 2 3

func (k *KMP) makeNext(pattern string) []int {
	k.pattern = pattern
	k.next = make([]int, len(pattern))

	for i, j := 1, 0; i < len(pattern); i++ {
		for j > 0 && pattern[j] != pattern[i] {
			j = k.next[j-1]
		}

		if pattern[j] == pattern[i] {
			j++
		}
		k.next[i] = j
	}

	return k.next
}

func (k *KMP) find(s string) []int {
	j := 0
	res := []int{}
	for i, c := range s {
		for j > 0 && c != int32(k.pattern[j]) {
			j = k.next[j-1]
		}
		if c == int32(k.pattern[j]) {
			j++
		}
		if j == len(k.pattern) {
			res = append(res, i-len(k.pattern)+1)
			j = k.next[j-1]
		}
	}

	return res
}

func removeOccurrences(s string, part string) string {
	kmp := &KMP{}
	kmp.makeNext(part)
	//fmt.Println("00")
	//fmt.Println(s)

	for r := kmp.find(s); len(r) > 0; r = kmp.find(s) {
		s = s[0:r[0]] + s[r[0]+len(part):]
		// fmt.Println(s)
	}

	return s
}

六、总结

主要内容：

  1. 本文详细介绍了KMP原理，对推论进行了证明。

  2. 作用：查询子串，查询字符串是否为循环，查询最长公共前缀后缀。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

七、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动手把刚才的题A了。

  1. 子串查询 力扣
  2. next数组应用：力扣
  3. 子串查询：dcvhttps://leetcode-cn.com/problems/remove-all-occurrences-of-a-substring/

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

https://leetcode-cn.com/problemset/algorithms/?page=1&topicSlugs=string-matching 字符串匹配，有些不能用KMP。

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

hdu

以下将序号替换就是题目链接。

  1. Problem - 1238
  2. Problem - 1358
  3. Problem - 1686
  4. Problem - 1711
  5. https://acm.hdu.edu.cn/showproblem.php?pid=2609
  6. Problem - 2087
  7. https://acm.hdu.edu.cn/showproblem.php?pid=2203
  8. Problem - 2328
  9. Problem - 2594
  10. Problem - 3336
  11. https://acm.hdu.edu.cn/showproblem.php?pid=3374
  12. https://acm.hdu.edu.cn/showproblem.php?pid=3746
  13. Problem - 4300

Poj

以下将序号替换就是题目链接。

  1. 2406 -- Power Strings
  2. 2752 -- Seek the Name, Seek the Fame
  3. 3080 -- Blue Jeans

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。

在这里插入图片描述

2

案例2你写复杂了 半天没读懂 ! 可以直接return p[0,next[-1]] 这个性质就可以
附录代码

package main

import "fmt"

func next(p string) (ans string) {

	// 1. 宁可多开辟也不要少开辟!
	nxt := make([]int, len(p)+1)
	nxt[0] = 0
	ans = ""
	for i, j := 1, 0; i < len(p); i++ {
		for j > 0 && p[i] != p[j] {
			j = nxt[j]
		}
		if p[i] == p[j] {
			j++
		}
		nxt[i+1] = j
	}
	if nxt[len(p)] != 0 {
		ans = p[0:nxt[len(p)]]
	}
	return
}

func main() {
	s := "leetcodeleet"
	//s = "a"
	//s = "level"
	fmt.Println(next(s))
}