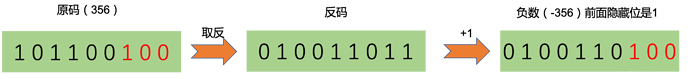AK F.*ing leetcode 流浪计划之树状数组

[LightningBilly]

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。
@[toc]

零、简介

之前有介绍过前缀和，它的作用是可以在O(1)时间内求出区间和。它的缺点只能处理固定的数组，如果是可变数组的区间和就处理不了。树状数组就是用来处理可变数组区间求和问题。

树状数组利用二进制思想对数组进行分组，可以做到log(n)复杂度完成一次更新和查询。

树状数组除了在底层实现上与前缀和不一样，在求和的用法上和前缀和基本一样。

在一维数组基础上，可以扩展到二维数组的情况。

树状数组实现起来代码也比较简洁，不过其原理理解起来比较麻烦。本文将介绍开根号分组法（帮助理解），进而重点介绍树状数组，再实现一些常用的算法模板。

一、分组思想

先来看一个经题目

链接：力扣

题目大意

给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。

实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], …, nums[right]）

示例：

输入：
[“NumArray”, “sumRange”, “update”, “sumRange”]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 9 ，sum([1,3,5]) = 9
numArray.update(1, 2); // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 8 ，sum([1,2,5]) = 8

提示：

1 <= nums.length <= 3 * 10^4
-100 <= nums[i] <= 100
0 <= index < nums.length
-100 <= val <= 100
0 <= left <= right < nums.length
最多调用 3 * 10^4 次 update 和 sumRange 方法

解法一 朴素做法

每次更新就直接更新数组的值。查询的时候需要对区间内数字加和。

复杂度：每次更新O(1)，每次查询O(n) 总体复杂度O(n^2)。

结论：复杂度过高。

解法二 引入前缀和

PreSum[i] = \sum_{i=0}^Narr[i]\\ 求解区间和\ sumRange(i,j) = PreSum[j]-PreSum[i-1]

每次更新需要对影响到的前缀和更新。例如，更新arr[i] = x，那么需要更新presum[j] += x-arr[i] (j>=i)。

每次查询只需要O(1), 总体复杂度依然是O(n^2)。

结论：复杂度过高。

解法三 分组计算

上述2种方法，更新与查询，总有一个操作是O(n), 导致最后的复杂度是O(n^2)。

原因是操作的对象太细，总数就太多了。

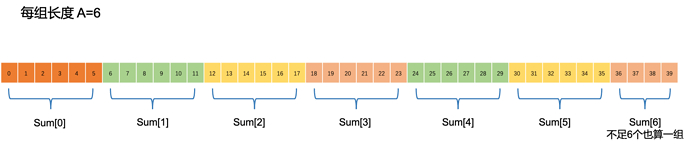
我们把数组按连续的a个数字进行分组。每组的和用Sum[i]表示。

Sum[i]=\sum_{x=i*a}^{(i+1)*a-1}arr[x] \\ ----------------------------------- \\ 展开如下\ \ \ \underbrace{arr[i*a]+arr[i*a+1]+...+arr[i*a+a-2]+arr[i*a+a-1]}_{Sum[i]}

当更新arr[i]=x时，需要更新 sum[i/a] += x-arr[i] (sum[i/a] 刚好包含arr[i])

这样更新的复杂度是O(1)

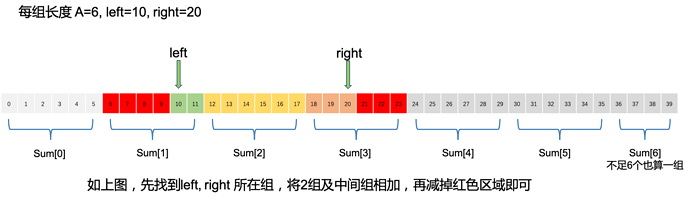
查询时，从包含第一个元素的Sum[i]开始加到最后一个包含元素的Sum[i]。

再把多余的数字单独减掉。

求解区间和 sumRange(i,j) = \sum_{x=\lfloor i/a \rfloor}^{\lfloor j/a\rfloor}sum[x]\ -\ \sum_{x= (\lfloor i/a \rfloor-1) *a}^{i-1}arr[x]\ - \ \sum_{x= j+1}^{(\lfloor j/a \rfloor+1) *a-1}arr[x]

从上式可以看出，求和复杂度是分组组数+每组个数 = O(len(arr)/a+a)

复杂度的大小取决于a的值。那么a取多少合适呢。

转化一下 y=n/a+a, n是固定值，a的取值范围是1到n，问a取多少时整体y最小。

对y进行求导

y'=- \frac{n}{a^2}+1 \\ 当a\in[1,\sqrt n) 时，y'<0, 说明y一直在减小 \\ a=\sqrt n时到达最小值。\\ 之后 y'>0, y又开始增大。\\ 故a越接近 \sqrt n， y越小 \\ 令a= \lfloor \sqrt n \rfloor 即可 \\ 此时总体复杂度为O(n \sqrt n)。 题目中最大规模为3*10^4，\\ 算下来规模是10^6可以接受。

AC代码

type NumArray struct {
	/*
		a 代表每组多少个
		sum[i] = nums[i*a]+nums[i*a+1]+...+nums[i*a+a-1]
		nums[i] 属于sum[i/a]
	*/
	sum  []int
	a    int
	nums []int
}

func Constructor(nums []int) NumArray {
	a := int(math.Sqrt(float64(len(nums))))
	na := NumArray{
		sum:  make([]int, len(nums)/a+1), // 初始化长度
		nums: nums,
		a:    a,
	}

	// 计算sum值
	for i, v := range nums {
		na.sum[i/a] += v
	}

	return na
}

func (this *NumArray) Update(index int, val int) {
	// 更新 index所在组，sum[index/a] += val-nums[index]
	this.sum[index/this.a] += val - this.nums[index]
	this.nums[index] = val
}

func (this *NumArray) SumRange(left int, right int) int {
	/*
	   把 sum 从 left/a 到 right/a 先加起来，
	   然后把头尾多余出来的减掉。
	*/
	res := 0
	for i := left / this.a; i <= right/this.a; i++ {
		res += this.sum[i]
	}

	// 减去头部
	for i := left / this.a * this.a; i < left; i++ {
		res -= this.nums[i]
	}
	// 减去尾部, 注意最后一组可能会越界要判断一下
	for i := right + 1; i < (right/this.a+1)*this.a && i<len(this.nums); i++ {
		res -= this.nums[i]
	}

	return res
}

/**
 * Your NumArray object will be instantiated and called as such:
 * obj := Constructor(nums);
 * obj.Update(index,val);
 * param_2 := obj.SumRange(left,right);
 */
/*
cases:
["NumArray","sumRange","update","sumRange"]
[[[1,3,5]],[0,2],[1,2],[0,2]]
["NumArray","sumRange","update","sumRange"]
[[[1]],[0,0],[0,2],[0,0]]
["NumArray","sumRange","sumRange","sumRange","update","sumRange","sumRange","update","sumRange"]
[[[1,2,3,4,5,6,7,8,9,10]],[0,9],[1,8],[2,7],[0,9],[3,6],[4,5],[5,5],[5,5]]
*/

解法四 树状数组

树状数组是在上面分组的基础上对分组的大小进行更细粒度的划分，可以达到每次操作log(n)复杂度。

下面我们来介绍一下它。

二、定义

树状数组的基础数据结构很简单就是一个数组sum[]

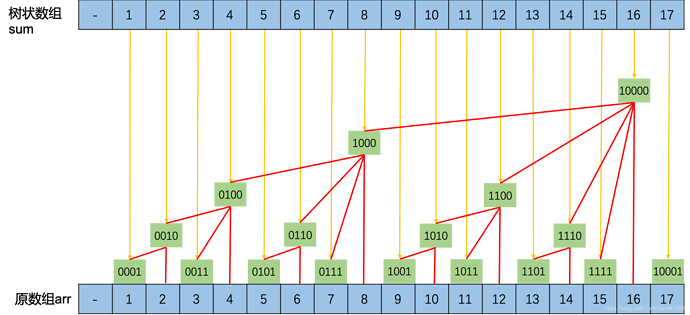
每个sum[i]表示和的范围都不一样。我们用图来看一下。

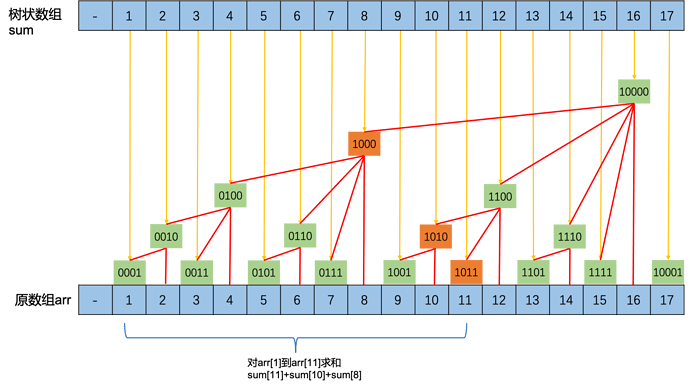
下面的数组是原数组，上面的树状数组表示。绿色框里面树状数组编号的二进制表示。

0号位置不用。

数组状数组的巧妙之处就在它的二进制数据中。

我们先来看一下sum[i]的定义。

• sum[1] = arr[1];
• sum[2] = arr[1] + arr[2];
• sum[3] = arr[3];
• sum[4] = arr[1] + arr[2] + arr[3] + arr[4];
• sum[5] = arr[5];
• sum[6] = arr[5] + arr[6];
• sum[7] = arr[7];
• sum[8] = arr[1] + arr[2] + arr[3] + arr[4] + arr[5] + arr[6] + arr[7] + arr[8];

可以发现，这颗树是有规律的

sum[i]=\sum_{x=i-k+1}^{i}(k是i的二进制最后一个1和后面的0所组成数字的大小)\\ 例如 i=6时，二进制表示为110，最后的10进制为2,则 \\ sum[6]=\sum_{x=6-2+1}^6arr[x] = arr[5]+arr[6] \\ 可以看出 sum[i]包含的最后一个元素就是arr[i], 往前延伸的长度就是k。

光看红色的线，是不是很像一棵树，这也是树状数组名字的由来。

二进制除了sum[i]包含的元素个数外，还反映出另一个信息。就是sum[i]会被后面的哪个sum结点所包含（即父结点）。

随便一个结点，沿红色线向上查找到最近一个结点，然后将两结点编号之差就是刚才说的k。

举例，i=12, 沿红线往上走，遇到的是编号16，两者相差是4，12二进制最低位1和0组成的是100刚好是4。

所以，编号里隐含了2个重要信息，当前结点存储的长度，和假如更新当前结点，影响的下一个结点（父结点）相距多远。对应到同一个数字。

三、作用

1. 主要作用是求区间和。
2. 与前缀和相比，其最大的特点是可以处理多次可变的数组区间和。
3. 可以处理二维数组的情况。
4. 结合差分可以解决区间修改，区间和查询。
5. 配合二分思想可以做很多动态数组查询问题，比如第K大数字，最大值，最小值。
6. 结合数字离散化，可以解决很多计数问题。

四、数据定义及算法

树状数组，顾名思义是用数组来表示的。

主要有更新和求区间和2种操作。

数据定义

TreeArray {
    sum array // 数组 编号从1开始
  	n int // 数组大小
    // 主要操作：
	  Init(int): // 初始化，申请数组大空间。
	  Add(int,int): //更新操作
	  QueryPre(int):// 求前缀和
	  QuerySum(int,int): // 求区间和
}

算法描述

初始化

Init(l int) {
	sum <- [l]int
	n <- l
}

更新操作

这里的更新操作是对某个元素进行加或减操作，直接赋值操作需要转化成加减操作。

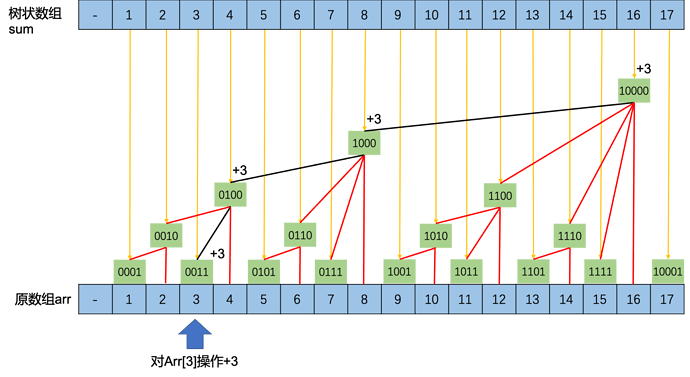
当我们对某个元素进行操作后，那么sum数组中被影响到的结点都要更新。

以Arr[3]+=3为例，那么 如图中沿黑线往 上找到的结点都要更新sum[3], sum[4], sum[8], sum[16]都是被影响到的结点，都要+3。

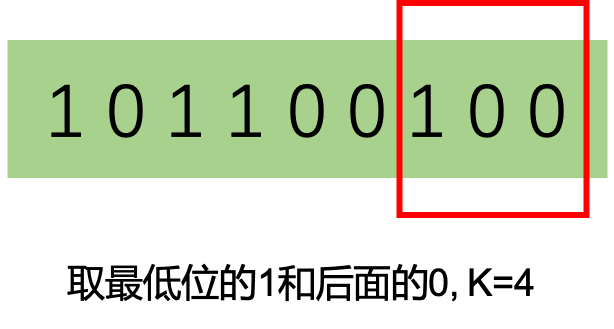
那么怎么找呢，就要用到上文中计算K的原理了。需要找到二进制中最低位的1.

比较直接的就是移位法，查询x中k的值如下

getLowBit(x):
	i=1
	while x&i==0 {
		i<<=1
	}
	return i

还可以利用(x-1)&x的作用是把最后一个1变成0的原理。

getLowBit(x):
	return x - ((x-1)&x)

官方给出的方法是

getLowBit(x):
	return x & (-x)
	

原理是负数的二进制是原数的反码加1。刚好除了最低位1和后面的0是一样的，其他位都是相反的。如图：

负数表示的原理如下，以32位为例，以0为基准。

0 = \underbrace {1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111}_{32个1} \ \ 最高位是1\\ -1 = 0-1 = \underbrace {1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1111\ \ 1110}_{31个1+1个0} \\ 就是挖空一些位置，而这些挖空的值刚好是与0的差值。

// 更新算法
add(i, a): // 更新 arr[i] +=a
	for ;i<=n;i+=getLowBit(i) { // 沿着线往上找影响到的结点，并更新
		sum[i]+=a
	}

计算前缀和

与更新相反，求和是从上到下的一个过程。

以求 preSum(11)为例。图中橙色块就是要加的对象。

先加sum[11], 计算出sum[11]中元素的长度getLowBit（11）=1， 11-1=10

再加sum[10], 同理计算出lowbit = 2， 10-2=8

再加sum[8], 同理计算出lowbit = 8, 8-8=0 算法结束。

// 求前缀和
QueryPre(i):
	res = 0
	for ;i>0;i-=getLowBit(i){
		res += sum[i]
	}
	return res
	
// 求区间和
QuerySum(i,j):
	return QueryPre(j)-QueryPre(i-1)

二维数组情况可以参考

https://baike.baidu.com/item/二维树状数组/20415329?fr=aladdin

https://blog.csdn.net/zzti_xiaowei/article/details/81053094

五、具体实现

func getLowBit(x int) int {
	return x & (-x)
}

type TreeArray struct {
	sum []int // 数组 编号从1开始
	n   int   // 数组大小
}

// 初始化，申请数组大空间。
func (t *TreeArray) Init(n int) {
	t.n = n
	t.sum = make([]int, n+1) // 0号元素不用，n号元素需要使用
}

//更新操作
func (t *TreeArray) Add(x, v int) {
	for ; x <= t.n; x += getLowBit(x) { // 沿着线往上找影响到的结点，并更新
		t.sum[x] += v
	}
}

// 求前缀和
func (t *TreeArray) QueryPre(i int) int {
	res := 0
	for ; i > 0; i -= getLowBit(i) {
		res += t.sum[i]
	}
	return res
}

// 求区间和
func (t *TreeArray) QuerySum(i, j int) int {
	return t.QueryPre(j) - t.QueryPre(i-1)
}

复杂度分析，每次add或sum 都是对数字的二进制进行移位，所以单次操作复杂度是log(n)

六、牛刀小试

练习1 可区间求和应用

链接：力扣

回到刚开始的题目

题目大意

略

题目解析

只要利用add做单点更新，用querysum求区间和就可以了

AC代码

func getLowBit(x int) int {
	return x & (-x)
}

type TreeArray struct {
	sum []int // 数组 编号从1开始
	n   int   // 数组大小
}

// 初始化，申请数组大空间。
func (t *TreeArray) Init(n int) {
	t.n = n
	t.sum = make([]int, n+1) // 0号元素不用，n号元素需要使用
}

//更新操作
func (t *TreeArray) Add(x, v int) {
	for ; x <= t.n; x += getLowBit(x) { // 沿着线往上找影响到的结点，并更新
		t.sum[x] += v
	}
}

// 求前缀和
func (t *TreeArray) QueryPre(i int) int {
	res := 0
	for ; i > 0; i -= getLowBit(i) {
		res += t.sum[i]
	}
	return res
}

// 求区间和
func (t *TreeArray) QuerySum(i, j int) int {
	return t.QueryPre(j) - t.QueryPre(i-1)
}

type NumArray struct {
	tree *TreeArray
	nums []int
}

/*
由于树状数组弃用0号元素，所以以下操作下标都要加1
 */
func getIndex(x int) int {
	return x+1
}

func Constructor(nums []int) NumArray {
	na := NumArray{
		tree: &TreeArray{},
		nums: nums,
	}
	na.tree.Init(len(nums))

	// 计算sum值
	for i, v := range nums {
		na.tree.Add(getIndex(i), v) // 注意下标转化
	}

	return na
}

func (this *NumArray) Update(index int, val int) {
	// 更新 差值
	this.tree.Add(getIndex(index),  val - this.nums[index])
	this.nums[index] = val
}

func (this *NumArray) SumRange(left int, right int) int {
	return this.tree.QuerySum(getIndex(left), getIndex(right)) // 直接调用求区间和
}
/*
cases:
["NumArray","sumRange","update","sumRange"]
[[[1,3,5]],[0,2],[1,2],[0,2]]
["NumArray","sumRange","update","sumRange"]
[[[1]],[0,0],[0,2],[0,0]]
["NumArray","sumRange","sumRange","sumRange","update","sumRange","sumRange","update","sumRange"]
[[[1,2,3,4,5,6,7,8,9,10]],[0,9],[1,8],[2,7],[0,9],[3,6],[4,5],[5,5],[5,5]]
*/

练习2 离散化计数 统计作战单位数

题目链接：力扣

题目大意

n 名士兵站成一排。每个士兵都有一个 独一无二 的评分 rating 。

每 3 个士兵可以组成一个作战单位，分组规则如下：

从队伍中选出下标分别为 i、j、k 的 3 名士兵，他们的评分分别为 rating[i]、rating[j]、rating[k]
作战单位需满足： rating[i] < rating[j] < rating[k] 或者 rating[i] > rating[j] > rating[k] ，其中 0 <= i < j < k < n
请你返回按上述条件可以组建的作战单位数量。每个士兵都可以是多个作战单位的一部分。

示例 1：

输入：rating = [2,5,3,4,1]
输出：3
解释：我们可以组建三个作战单位 (2,3,4)、(5,4,1)、(5,3,1) 。
示例 2：

输入：rating = [2,1,3]
输出：0
解释：根据题目条件，我们无法组建作战单位。
示例 3：

输入：rating = [1,2,3,4]
输出：4

提示：

n == rating.length
3 <= n <= 1000
1 <= rating[i] <= 10^5
rating 中的元素都是唯一的

题目解析

先把题目简化一下给定士兵i 求排在i前面并且rating比 rating[i]小的士兵个数。

这里有2个维度，坐标的大小，rating的大小。

一般这种题目可以从前往后遍历，当前遍历到的士兵的坐标都是比之前大的，就解决了坐标大小的问题。

再看tating统计。其实就是查询之前遍历过的rating里比当前raging小的个数。

如果把rating统计到一个数组 cnt[] 每遍历一个rating[i]，cnt[rating[i]]++, 想查询<rating[i]的个数时。

其实就是

当cnt数组里<rating[i]的个数 = \sum_{x=0}^{rating[i]-1}cnt[x]

这一看不就是前缀和么。而且是一个可变数组的前缀和。可以使用树状数组解决。

解决了所有士兵排在他前面且rating比他小的计数问题后。假设结果数组是Res1[]。

再来看rating[i] < rating[j] < rating[k] （0 <= i < j < k < n）。

可以再利用上述思想，从前往后遍历，然后统计cnt[rating[i]]+=res1[i]。

rating[i] < rating[j] < rating[k] 的总数 = \sum_{x=0}^{rating[k]-1}cnt[x]

依然是求前缀和，可以使用树状数组解决。

对于 rating[i] > rating[j] > rating[k] 也可以如法炮制，只不过求和区间要改一下。

\sum_{x=rating[k]+1}^{10^5}cnt[x]

查询比自己大的计数范围，依然是区间和。

AC代码

func getLowBit(x int) int {
	return x & (-x)
}

type TreeArray struct {
	sum []int // 数组 编号从1开始
	n   int   // 数组大小
}

// 初始化，申请数组大空间。
func (t *TreeArray) Init(n int) {
	t.n = n
	t.sum = make([]int, n+1) // 0号元素不用，n号元素需要使用
}

//更新操作
func (t *TreeArray) Add(x, v int) {
	for ; x <= t.n; x += getLowBit(x) { // 沿着线往上找影响到的结点，并更新
		t.sum[x] += v
	}
}

// 求前缀和
func (t *TreeArray) QueryPre(i int) int {
	res := 0
	for ; i > 0; i -= getLowBit(i) {
		res += t.sum[i]
	}
	return res
}

// 求区间和
func (t *TreeArray) QuerySum(i, j int) int {
	return t.QueryPre(j) - t.QueryPre(i-1)
}

type NumArray struct {
	tree *TreeArray
	nums []int
}


func numTeams(rating []int) int {
	res1 , res2 := make([]int, len(rating)), make([]int, len(rating)) // 同时求出比自己大和小的计数。
	tree := &TreeArray{}
	tree.Init(1e5+10)
	for i, r := range rating {
		res1[i] = tree.QueryPre(r-1)
		res2[i] = tree.QuerySum(r+1, tree.n)
		tree.Add(r, 1)
	}

	sum :=0
	// 先求 rating[i] < rating[j] < rating[k]
	tree.Init(1e5+10) // 要重新初始化
	for i,r:= range rating {
		sum += tree.QueryPre(r-1)
		tree.Add(r, res1[i])
	}

	// 再求 rating[i] > rating[j] > rating[k]
	tree.Init(1e5+10) // 要重新初始化
	for i,r:= range rating {
		sum += tree.QuerySum(r+1, tree.n)
		tree.Add(r, res2[i])
	}

	return sum
}

练习3 查询带键的排列

题目链接：力扣

题目大意

给你一个待查数组 queries ，数组中的元素为 1 到 m 之间的正整数。 请你根据以下规则处理所有待查项 queries[i]（从 i=0 到 i=queries.length-1）：

一开始，排列 P=[1,2,3,…,m]。
对于当前的 i ，请你找出待查项 queries[i] 在排列 P 中的位置（下标从 0 开始），然后将其从原位置移动到排列 P 的起始位置（即下标为 0 处）。注意， queries[i] 在 P 中的位置就是 queries[i] 的查询结果。
请你以数组形式返回待查数组 queries 的查询结果。

示例 1：

输入：queries = [3,1,2,1], m = 5
输出：[2,1,2,1]
解释：待查数组 queries 处理如下：
对于 i=0: queries[i]=3, P=[1,2,3,4,5], 3 在 P 中的位置是 2，接着我们把 3 移动到 P 的起始位置，得到 P=[3,1,2,4,5] 。
对于 i=1: queries[i]=1, P=[3,1,2,4,5], 1 在 P 中的位置是 1，接着我们把 1 移动到 P 的起始位置，得到 P=[1,3,2,4,5] 。
对于 i=2: queries[i]=2, P=[1,3,2,4,5], 2 在 P 中的位置是 2，接着我们把 2 移动到 P 的起始位置，得到 P=[2,1,3,4,5] 。
对于 i=3: queries[i]=1, P=[2,1,3,4,5], 1 在 P 中的位置是 1，接着我们把 1 移动到 P 的起始位置，得到 P=[1,2,3,4,5] 。
因此，返回的结果数组为 [2,1,2,1] 。
示例 2：

输入：queries = [4,1,2,2], m = 4
输出：[3,1,2,0]
示例 3：

输入：queries = [7,5,5,8,3], m = 8
输出：[6,5,0,7,5]

提示：

1 <= m <= 10^3
1 <= queries.length <= m
1 <= queries[i] <= m

题目解析

先用模拟法做一下，把数组设置成2*m长度，把数字都入到后面一半中。

一开始数组如下

arr = [0,0,0…,0, 1, 2, 3, 4, 5, 6,…,m]

维护一个索引map ind, 这样给出一个x可以很快知道在数组中的位置ind[x]。数一下前面有多少个数字。

然后把x放到前面 arr[m-i]=x, 原来的位置变成0arr[ind[x]]=0, ind[x] = m-i。

这样每次操作是O(n)。

主要的花费是在数数字上。

数数字的过程其实就是求某个位置前面有多少个数字。如果把有数字的地方设置成1，其实就是求前缀和。

可以设置arr = [0,0,0,0,0…,0, 1, 1, 1, 1,…,1] 一开始有数字的地方为1，没数字的地方为0，后续移动数字就是+1，-1操作。统计就用前缀和。

AC代码

func getLowBit(x int) int {
	return x & (-x)
}

type TreeArray struct {
	sum []int // 数组 编号从1开始
	n   int   // 数组大小
}

// 初始化，申请数组大空间。
func (t *TreeArray) Init(n int) {
	t.n = n
	t.sum = make([]int, n+1) // 0号元素不用，n号元素需要使用
}

//更新操作
func (t *TreeArray) Add(x, v int) {
	for ; x <= t.n; x += getLowBit(x) { // 沿着线往上找影响到的结点，并更新
		t.sum[x] += v
	}
}

// 求前缀和
func (t *TreeArray) QueryPre(i int) int {
	res := 0
	for ; i > 0; i -= getLowBit(i) {
		res += t.sum[i]
	}
	return res
}

// 求区间和
func (t *TreeArray) QuerySum(i, j int) int {
	return t.QueryPre(j) - t.QueryPre(i-1)
}

type NumArray struct {
	tree *TreeArray
	nums []int
}


func processQueries(queries []int, m int) []int {
	tree := &TreeArray{}
	tree.Init(2*m)
	ind := map[int]int{}
	// 设置初始值，下标从1开始
	for i:=m+1;i<=2*m;i++ {
		ind [i-m]=i
		tree.Add(i, 1)
	}

	ans := make([]int, len(queries))
	for i, v := range queries {
		ans [i] = tree.QueryPre(ind[v]-1) // 统计前面有多少数字
		tree.Add(ind[v], -1) // 删除数字
		ind[v] = m-i // 更新下标
		tree.Add(ind[v], 1)
	}

	return ans
}

练习4 配合二分法求解第K大 求出 MK 平均值

题目链接：力扣

题目大意

给你两个整数 m 和 k ，以及数据流形式的若干整数。你需要实现一个数据结构，计算这个数据流的 MK 平均值 。

MK 平均值 按照如下步骤计算：

如果数据流中的整数少于 m 个，MK 平均值 为 -1 ，否则将数据流中最后 m 个元素拷贝到一个独立的容器中。
从这个容器中删除最小的 k 个数和最大的 k 个数。
计算剩余元素的平均值，并 向下取整到最近的整数 。
请你实现 MKAverage 类：

MKAverage(int m, int k) 用一个空的数据流和两个整数 m 和 k 初始化 MKAverage 对象。
void addElement(int num) 往数据流中插入一个新的元素 num 。
int calculateMKAverage() 对当前的数据流计算并返回 MK 平均数 ，结果需 向下取整到最近的整数 。

示例 1：

输入：
[“MKAverage”, “addElement”, “addElement”, “calculateMKAverage”, “addElement”, “calculateMKAverage”, “addElement”, “addElement”, “addElement”, “calculateMKAverage”]
[[3, 1], [3], [1], [], [10], [], [5], [5], [5], []]
输出：
[null, null, null, -1, null, 3, null, null, null, 5]

解释：
MKAverage obj = new MKAverage(3, 1);
obj.addElement(3); // 当前元素为 [3]
obj.addElement(1); // 当前元素为 [3,1]
obj.calculateMKAverage(); // 返回 -1 ，因为 m = 3 ，但数据流中只有 2 个元素
obj.addElement(10); // 当前元素为 [3,1,10]
obj.calculateMKAverage(); // 最后 3 个元素为 [3,1,10]
// 删除最小以及最大的 1 个元素后，容器为 [3]
// [3] 的平均值等于 3/1 = 3 ，故返回 3
obj.addElement(5); // 当前元素为 [3,1,10,5]
obj.addElement(5); // 当前元素为 [3,1,10,5,5]
obj.addElement(5); // 当前元素为 [3,1,10,5,5,5]
obj.calculateMKAverage(); // 最后 3 个元素为 [5,5,5]
// 删除最小以及最大的 1 个元素后，容器为 [5]
// [5] 的平均值等于 5/1 = 5 ，故返回 5

提示：

3 <= m <= 10^5
1 <= k*2 < m
1 <= num <= 10^5
addElement 与 calculateMKAverage 总操作次数不超过 10^5 次。

题目解析

题目每次要求统计的其实是当前m个数字。

那我们只要对当前每种数字进行计数就可以了。

设计数数组为cnt[] 长度是10^5。

每次来一个新数字x , cnt[x]++。

然后把前第m个数字 q, cnt[q]–。

求解平均值，先找到前面K个，后面K个。然后减掉。

这里要解决2个问题：

1. 每次有新数据进来后怎么知道前m个是什么。
2. 当前m个数字中最小K个。

问题1用队列可以解决，当队列到达m个时，就开始出队。

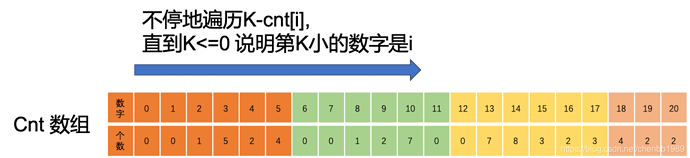
问题2 看图

其实就是找到 i 使得 cnt[1]+cnt[2]+cnt[3]+…+cnt[i]>=K 。

前面就是一个前缀和，前缀和是可以O(1)求出的。再配合2分，可以很快找到i，也可以知道前K个数字的和。

AC代码

/*

 */
type ArrTree struct {
	c []int
	n int
}

func ConstructArrTree(n int) *ArrTree {
	return &ArrTree{
		c: make([]int, n+1),
		n: n,
	}
}

func lowbit(x int) int { return x & (-x) }

func (tree *ArrTree) update(x, y int) {
	if x == 0 {
		return
	}
	for i := x; i <= tree.n; i += lowbit(i) {
		tree.c[i] += y
	}
}
func (tree *ArrTree) getsum(x int) int {
	ans := 0
	for i := x; i > 0; i -= lowbit(i) {

		ans += tree.c[i]
	}
	return ans
}

type MKAverage struct {
	sumTree   *ArrTree // 计总和 最小的k个数字的和
	countTree *ArrTree // 计数
	m, k      int
	arr       []int
}

func Constructor(m int, k int) MKAverage {
	return MKAverage{
		sumTree:   ConstructArrTree(int(1e5)+10),
		countTree: ConstructArrTree(int(1e5)+10),
		m:         m,
		k:         k,
		arr:       []int{},
	}
}

func (this *MKAverage) AddElement(num int) {
	this.arr = append(this.arr, num)
	this.sumTree.update(num, num)
	this.countTree.update(num, 1)

	if len(this.arr) > this.m {
		this.sumTree.update(this.arr[0], -this.arr[0])
		this.countTree.update(this.arr[0], -1)
		this.arr = this.arr[1:]
	}
}

// 二分法最小的第K个数字
func findLow(k int, tree *ArrTree) int {
	l, r := 0, tree.n
	best := 0

	for l <= r {
		mid := (l + r) / 2
		if tree.getsum(mid) <= k {
			best = mid
			l = mid + 1
		} else {
			r = mid - 1
		}
	}

	return best
}


func (this *MKAverage) CalculateMKAverage() int {
	if len(this.arr) < this.m {
		return -1
	}
	// 这里查找的是最小的K个，和最小的m-k个。
	low, high:= findLow(this.k, this.countTree), findLow(this.m-this.k, this.countTree)

	sum := this.sumTree.getsum(high) - this.sumTree.getsum(low)
	sum -= (low+1)*(this.k-this.countTree.getsum(low)) // 需要减掉重复的数字
	sum += (high+1)*(this.m-this.k- this.countTree.getsum(high)) // 需要加上少掉的部分。

	return sum/(this.m-2*this.k)
}

七、总结

主要内容：

1. 之前有介绍过前缀和，它的缺点只能处理固定的数组。树状数组就是用来处理可变数组区间求和问题。

   树状数组利用二进制思想对数组进行分组，可以做到log(n)复杂度完成一次更新和查询。

2. 作用：1）求动态数组区间和；2)经常可以用来解决计数问题 ；3）配合二分思想可以做很多动态数组查询问题，比如第K大数字，最大值，最小值。

在使用树状数组时，最大的特点是就是数组的长度是固定的，所以经常要对数据进行离散化。然后，转化到树状数组模型上。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

推荐阅读

二维数组情况可以参考

• 二维树状数组_百度百科

• https://blog.csdn.net/zzti_xiaowei/article/details/81053094

八、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动用把刚才那4题A了。

1. 可变区间求和应用 力扣
2. 离散化计数：力扣
3. 离散化计数：力扣
4. 配合二分法求解第K大: 力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

力扣 树状数组相关题目

---

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

hdu

以下将序号替换就是题目链接。

1. http://acm.hdu.edu.cn/showproblem.php?pid=1166
2. http://acm.hdu.edu.cn/showproblem.php?pid=1541
3. http://acm.hdu.edu.cn/showproblem.php?pid=1556
4. http://acm.hdu.edu.cn/showproblem.php?pid=2642
5. http://acm.hdu.edu.cn/showproblem.php?pid=3465
6. http://acm.hdu.edu.cn/showproblem.php?pid=4339
7. http://acm.hdu.edu.cn/showproblem.php?pid=6274

Poj

以下将序号替换就是题目链接。

1. 1195 -- Mobile phones
2. 1990 -- MooFest
3. 2155 -- Matrix
4. 2299 -- Ultra-QuickSort
5. 2481 -- Cows
6. 3067 -- Japan
7. 3321 -- Apple Tree
8. 3468 -- A Simple Problem with Integers