数学是计算机的重要基础,算法题中常常会用到数学知识,尤其是离散、具体的数学,以数论、排列组合、概率期望、多项式为代表,可以出现在几乎任何类别的题目中,所有题目涉及到的数学知识点都已标出,建议去oi-wiki 学习。
强烈建议小伙伴先尝试用非数学的常规解法思考以下题目(也许会更简单更好理解),再用数学的解法。
超级丑数 做这题之前先学习求质数的几种方法 (强烈建议掌握),之后只需要思考如何求出第n个即可.石子游戏 经典的石子游戏肯定是不能错过的,建议先用动态规划解一遍。
剪绳子 II leetcode中有许多类似的题目掌握其中的思想,就能解决许多类似的问题:
构造乘积数组 记得考虑特殊情况。
2 个赞
关于第一题斐波那契数列,我之前做了一个ppt ,大家可以参考下。
我也有一篇矩阵相关的题解 矩阵+快速幂求解递推问题
斐波那契数列
func fib(n int) int {
if n < 2 {
return n
}
p, q, r := 0, 1, 1
for i := 2; i <= n; i++ {
r = (p + q) % (1e9 + 7)
p = q
q = r
}
return r
}
pub struct Solution;
impl Solution {
pub fn multiply(a: [[i64; 2]; 2], b: [[i64; 2]; 2]) -> [[i64; 2]; 2] {
let mut c:[[i64; 2]; 2] = [[0,0],[0,0]];
for i in 0..2 {
for j in 0..2 {
c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % (1000000007)
}
}
c
}
pub fn pow(mut a :[[i64;2];2], n:i32)-> [[i64; 2]; 2] {
let mut c:[[i64; 2]; 2]= [[1,0],[0,1]];
let mut n = n;
while n>0{
if n&1 ==1{
c = Self::multiply(c, a);
}
a = Self::multiply(a, a);
// println!("{:?}",a);
n = n>>1;
}
c
}
pub fn fib(n: i32) -> i32 {
if n <2{
return n;
}
let r:[[i64; 2]; 2] = Self::pow([[1,1],[1,0]], n-1);
return r[0][0] as i32
}
}
#[cfg(test)]
mod tests {
use crate::Solution;
#[test]
fn it_works() {
assert_eq!(Solution::fib(5),5);
assert_eq!(Solution::fib(48),807526948);
assert_eq!(Solution::fib(6),8);
}
}
1 个赞
席乐朋
2021 年5 月 7 日 14:57
5
剑指 Offer 10- I. 斐波那契数列
func fib(n int) int {
if n < 2 {
return n
}
prev, curr := 0, 1
for i := 2; i <= n; i++ {
sum := prev + curr
prev = curr
curr = sum % 1000000007
}
return curr
}
509. 斐波那契数
func fib(n int) int {
if n == 0 || n == 1 {
return n
}
return fib(n-1) + fib(n-2)
}
复杂度分析
时间复杂度:O(2^n)。
空间复杂度:O(h)。
闭包写法:
func fib(n int) int {
memo := make([]int, n+1)//从0开始
var helper func(int) int
helper = func(n int) int {
if n == 0 || n == 1 {
return n
}
if memo[n] != 0 {
return memo[n]
}
memo[n] = helper(n-1) + helper(n-2)
return memo[n]
}
return helper(n)
}
func fib(n int) int {
memo := make([]int, n+1)
return helper(memo, n)
}
func helper(memo []int, n int) int {
if n < 2 {
return n
}
if memo[n] != 0 { //剪枝
return memo[n]
}
memo[n] = helper(memo, n-1) + helper(memo, n-2)
return memo[n]
}
复杂度分析
func fib(n int) int {
if n == 0 {
return 0
}
dp := make([]int, n+1)
dp[0], dp[1] = 0, 1 //base case
for i := 2; i <= n; i++ { //状态转移
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
复杂度分析
动态规划空间优化:只存储前2项
func fib(n int) int {
if n == 0 || n == 1 { //base case
return n
} //递推关系
prev, curr := 0, 1
for i := 2; i <= n; i++ {
next := prev + curr
prev = curr
curr = next
}
return curr
}
复杂度分析
1 个赞
席乐朋
2021 年5 月 9 日 00:38
8
谢谢欣赏

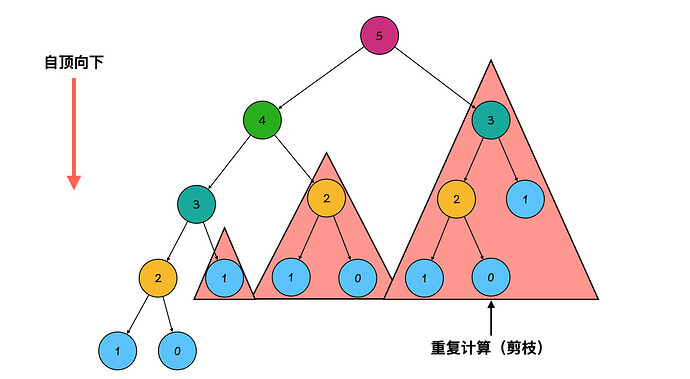
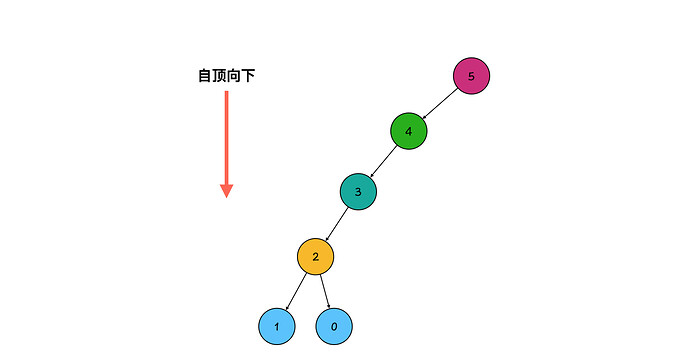
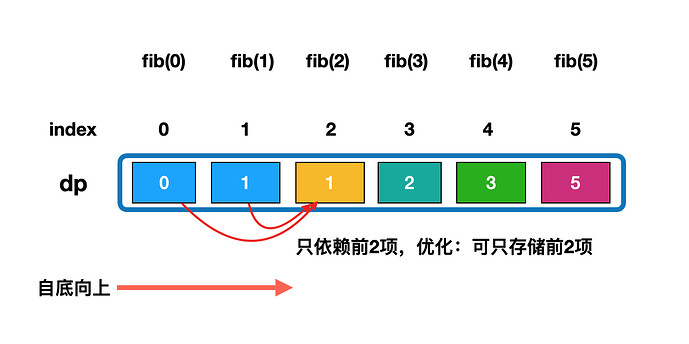
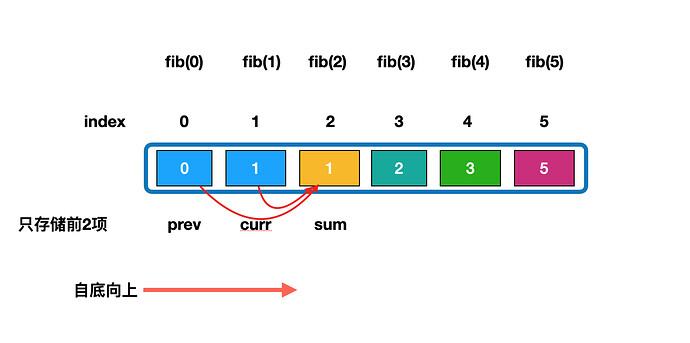

 Keynote 讲稿 (Mac ppt)
Keynote 讲稿 (Mac ppt)