AK F.*ing leetcode 流浪计划之堆

算法之美
,
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

@[toc]

一、简介

堆数据结构是一种数据选择器，基于其的排序算法其实是一种选择排序。堆在平时的算法中非常常用，也是go语言操作的基础算法。在面试中也经常被问到其原理，甚至会让手写堆排序。学习与解理堆算法原理，不管是对于语言排序源码的理解，还是解决算法题都是非常有帮助的。防止在面试时眼高手低。

由于堆实现在各语言中都有，这里主要以int为例，讲解堆原理，以及排序的实现。最后结合题目讲解堆的应用。

本文中堆原理参照严版《数据结构与算法》，公众号内回复“数据结构”可以获取pdf电子版。

二、定义

堆是一种完全二叉树数据结构。

其性质是二叉树中的每个子树，根的值总是要比孩子的值要大（大顶堆）。

堆有大顶堆与小顶堆之分，以堆顶元素是所有元素中最大或最小为区分。

完全二叉树在表示时我们可以用数组来表示（下标从1开始），结点i的2个孩子（如果有）分别2*i, 2*i+1。

堆的主要操作有，初始化堆，向下调整，向上调整，删除堆顶元素，添加一个元素。

三、作用

  1. 对元素进行排序。
  2. 快速选择最优值（最小，最大，条件最优等，dijkstra最短路应用）。
  3. 取集合中前K大元素。
  4. 通过定义多维条件，快速选择出最优解。

四、数据定义及算法

堆是一种完全二叉树数据结构。我们以下将以大顶为进行讲解。

在表示时我们可以用数组来表示（下标从1开始），结点i的2个孩子（如果有）分别2*i, 2*i+1。

数据定义

Heap {
    arr array // 数组 结点i的2个孩子（如果有）分别2\*i, 2*i+1。编号从1开始
    // 主要操作：
    down(i)：// 向下调整 
    up(i) // 向上调整 down, up是堆的基础操作，作用是在堆发生变化时，对堆进行调整，使得堆满足其性质
    Init(): // 初始化数据，通过多次调用down操作，使得数组满足堆的性质
  	Pop() // 弹出堆顶
	  Push(x) // 添加元素
}

算法描述

图1
图11699×974 92.7 KB

图2
图21747×929 79.5 KB 

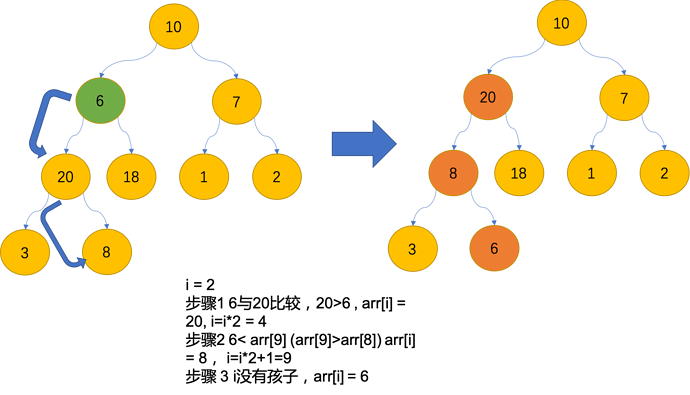
down(i): // 向下调整, 如图1
	pivot <- arr[i]
	while i*2<len(arr) : // 有子孩子
		child <- i*2
		如果有右孩子且右孩子值比左孩子大 child++
		如果孩子是否比根大：arr[i]<-arr[child], i <- child // 将根下移
		否则 break
	
	// 最后要把pivot赋值给最终根
	arr[i]<-pivot
		

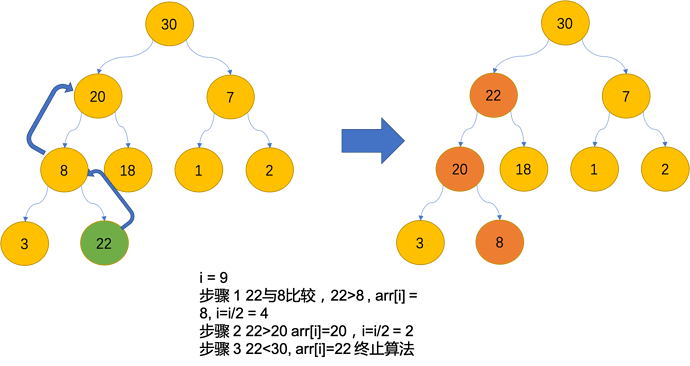
up(i): // 向上调整, 如图2
	pivot <- arr[i]
	while i/2 > 0 &&  arr[i/2]<pivot : // 有父结点且父值比自己的小
		arr[i]<-arr[i/2]
		i <- i/2
	
	// 最后要把pivot赋值给最终根
	arr[i]<-pivot
		

Init(arr): // 初始化数据，构建初始堆
    // 从n/2 编号开始，依次向下调整
    // 当调整至i，时i的所有子树已经调整完毕，所以只要关注arr[i]的位置，就可以使子树i形成堆。
    for i <- (len(arr)-1)/2 to 1 do
        down(i)

Pop():// 删除堆顶元素
	pivot <- arr[1]
	arr[1]<-arr[len(arr)-1] // 将最后一个值放到根
	arr <- arr[0:len(arr)-1] // 缩短最后一个空间
  
  down(1) // 向下调整
  return pivot


Push(x):// 添加元素
	arr <- append(arr, x)// 将最后一个值放到根
    up(len(arr)-1) // 向上调整

五、具体实现

package main
import "fmt"

type Heap struct {
	arr []int // 数组 结点i的2个孩子（如果有）分别2\*i, 2*i+1。编号从1开始
}

func (h *Heap) down(i int) { // 向下调整
	if i> h.Len() {return}
	pivot := h.arr[i]
	for i*2 <= h.Len() { // 有子孩子
		child := i * 2
		// 如果有右孩子且右孩子值比左孩子大
		if child+1 <= h.Len() && h.arr[child+1] > h.arr[child] {
			child++
		}

		// 如果孩子是否比根大：arr[i] <- arr[child], i <- child // 将根下移
		if h.arr[child] > pivot {
			h.arr[i], i = h.arr[child], child
		} else {
			break
		}

	}
	// 最后要把pivot赋值给最终根
	h.arr[i] = pivot
}

func (h *Heap) up(i int) { // 向上调整 down, up是堆的基础操作，作用是在堆发生变化时，对堆进行调整，使得堆满足其性质
	pivot := h.arr[i]
	for i/2 > 0 && h.arr[i/2] < pivot { // 有父结点且父值比自己的小
		h.arr[i], i = h.arr[i/2], i/2
	}

	// 最后要把pivot赋值给最终根
	h.arr[i] = pivot
}

func (h *Heap) Init(arr []int) { // 初始化数据，构建初始堆
	h.arr = append([]int{0}, arr...) // 第1个空元素，有效编号从1开始
	// 从n/2 编号开始，依次向下调整
	// 当调整至i，时i的所有子树已经调整完毕，所以只要关注arr[i]的位置，就可以使子树i形成堆。
	for i := h.Len()/ 2; i > 0; i-- {
		h.down(i)
	}
}

func (h *Heap) Len() int { // 获取元素个数
	if len(h.arr) < 2 {
		return 0
	}
	return len(h.arr) - 1
}

func (h *Heap) Pop() int { // 删除堆顶元素
	if h.Len() == 0 {
		panic("len == 0")
	}
	pivot := h.arr[1]
	h.arr[1] = h.arr[h.Len()]  // 将最后一个值放到根
	h.arr = h.arr[0 : h.Len()] // 缩短最后一个空间

	h.down(1) // 向下调整
	return pivot
}

func (h *Heap) Push(x int) { // 添加元素
	h.arr = append(h.arr, x) // 将最后一个值放到根
	h.up(h.Len())     // 向上调整
}

// 排序实现
func Sort(arr []int) []int{
	h := &Heap{}
	h.Init(arr)

	for i:=len(arr)-1;h.Len()>0;i-- {
		arr[i]=h.Pop() // 从大到小赋值
	}

	return arr
}

func main() {
   fmt.Println(Sort([]int{10,6,7,12,18,12,1,2,4,3}))
}

复杂度分析，每次up或down 都是二叉树高度，也就是 log(n), 堆的初始化是 nlog(n), 每次插入或删除是log(n)

以上代码只是为了理解堆排序原理作的简单实现，扩展性不好，实际应用可以直接使用go语言库。

六、牛刀小试

练习1 验证代码是否正确，排序应用

题目链接 力扣

题目大意

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

题目解析

原意是希望选手使用链表，这里是为了验证本文代码正确性。先转化成数组，然后利用堆排序，再赋值回链表。

AC代码

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */

type Heap struct {
	arr []int // 数组 结点i的2个孩子（如果有）分别2\*i, 2*i+1。编号从1开始
}

func (h *Heap) down(i int) { // 向下调整
	if i> h.Len() {return}
	pivot := h.arr[i]
	for i*2 <= h.Len() { // 有子孩子
		child := i * 2
		// 如果有右孩子且右孩子值比左孩子大
		if child+1 <= h.Len() && h.arr[child+1] > h.arr[child] {
			child++
		}

		// 如果孩子是否比根大：arr[i] <- arr[child], i <- child // 将根下移
		if h.arr[child] > pivot {
			h.arr[i], i = h.arr[child], child
		} else {
			break
		}

	}
	// 最后要把pivot赋值给最终根
	h.arr[i] = pivot
}

func (h *Heap) up(i int) { // 向上调整 down, up是堆的基础操作，作用是在堆发生变化时，对堆进行调整，使得堆满足其性质
	pivot := h.arr[i]
	for i/2 > 0 && h.arr[i/2] < pivot { // 有父结点且父值比自己的小
		h.arr[i], i = h.arr[i/2], i/2
	}

	// 最后要把pivot赋值给最终根
	h.arr[i] = pivot
}

func (h *Heap) Init(arr []int) { // 初始化数据，构建初始堆
	h.arr = append([]int{0}, arr...) // 第1个空元素，有效编号从1开始
	// 从n/2 编号开始，依次向下调整
	// 当调整至i，时i的所有子树已经调整完毕，所以只要关注arr[i]的位置，就可以使子树i形成堆。
	for i := h.Len()/ 2; i > 0; i-- {
		h.down(i)
	}
}

func (h *Heap) Len() int { // 获取元素个数
	if len(h.arr) < 2 {
		return 0
	}
	return len(h.arr) - 1
}

func (h *Heap) Pop() int { // 删除堆顶元素
	if h.Len() == 0 {
		panic("len == 0")
	}
	pivot := h.arr[1]
	h.arr[1] = h.arr[h.Len()]  // 将最后一个值放到根
	h.arr = h.arr[0 : h.Len()] // 缩短最后一个空间

	h.down(1) // 向下调整
	return pivot
}

func (h *Heap) Push(x int) { // 添加元素
	h.arr = append(h.arr, x) // 将最后一个值放到根
	h.up(h.Len())     // 向上调整
}

func Sort(arr []int) []int{
	h := &Heap{}
	h.Init(arr)

	for i:=len(arr)-1;h.Len()>0;i-- {
		arr[i]=h.Pop()
	}

	return arr
}

func sortList(head *ListNode) *ListNode {
	arr := []int{}
	for t:=head;t!=nil;t=t.Next {
		arr  = append(arr, t.Val)
	}

	arr = Sort(arr)
	for t:=head;t!=nil;t=t.Next {
		t.Val = arr[0]
		arr = arr[1:]
	}
	
	return head
}

练习2 利用小顶堆求丑数

题目链接：力扣

题目大意

给你一个整数 n ，请你找出并返回第 n 个 丑数 。

丑数 就是只包含质因数 2、3 和/或 5 的正整数。

示例 1：

输入：n = 10
输出：12
解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
示例 2：

输入：n = 1
输出：1
解释：1 通常被视为丑数。

提示：

1 <= n <= 1690

题目解析

每个丑数x, 都可以产生出3个丑数 x*2, x*3, x*5，产生后往池（丑数池里）里加。

下一个丑数是丑数池里最小的数。

从1开始 → 2,3,5

下一个选择的是2， 由于3，5都还未被选择到，所以以3，5为乘数的丑数是不可能被选择的。

AC代码

type myHeap []int

func (h *myHeap) Less(i, j int) bool {
	return (*h)[i] < (*h)[j]
}

func (h *myHeap) Swap(i, j int) {
	(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

func (h *myHeap) Len() int {
	return len(*h)
}

func (h *myHeap) Pop() (v interface{}) {
	*h, v = (*h)[:h.Len()-1], (*h)[h.Len()-1]
	return
}

func (h *myHeap) Push(v interface{}) {
	*h = append(*h, v.(int))
}

func nthUglyNumber(n int) int {
	h:= &myHeap{}
	heap.Push(h, 1) // 先加入1

	ans :=0
	for ;n>0;n-- {
		top := heap.Pop(h).(int)
		for top==ans {
			top = heap.Pop(h).(int)
		}
		ans = top
		//fmt.Println(ans)
    // 每产生一个丑数，就加入以该丑数为底数的更大的丑数
		heap.Push(h, ans*2)
		heap.Push(h, ans*3)
		heap.Push(h, ans*5)
	}

	return ans
}

练习3 利用条件构造解决复杂问题

题目链接：力扣

题目大意

给你一个按升序排序的整数数组 num（可能包含重复数字），请你将它们分割成一个或多个长度至少为 3 的子序列，其中每个子序列都由连续整数组成。

如果可以完成上述分割，则返回 true ；否则，返回 false 。

示例 1：

输入: [1,2,3,3,4,5]
输出: True
解释:
你可以分割出这样两个连续子序列 :
1, 2, 3
3, 4, 5
示例 2：

输入: [1,2,3,3,4,4,5,5]
输出: True
解释:
你可以分割出这样两个连续子序列 :
1, 2, 3, 4, 5
3, 4, 5
示例 3：

输入: [1,2,3,4,4,5]
输出: False

提示：

1 <= nums.length <= 10000

题目解析

定义数组 d[]，表示一个以d[0]结尾并且长度d[1]的序列。

遍历数组，去构造序列，每遇到一个数字x，优先查看是不可以加入到之前构造出来的序列。

利用贪心原理，优先查找d[0]=x-1, 并且d[1]最小的d. 这就可以通过堆来实现。

AC代码

type myHeap [][2]int

func (h *myHeap) Less(i, j int) bool {
	if (*h)[i][0] != (*h)[j][0] {
		return (*h)[i][0] < (*h)[j][0]
	} // 先取结尾数小的
	return (*h)[i][1] < (*h)[j][1] // 再取连续个数最小的
}

func (h *myHeap) Swap(i, j int) {
	(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

func (h *myHeap) Len() int {
	return len(*h)
}

func (h *myHeap) Pop() (v interface{}) {
	*h, v = (*h)[:h.Len()-1], (*h)[h.Len()-1]
	return
}

func (h *myHeap) Push(v interface{}) {
	*h = append(*h, v.([2]int))
}

func isPossible(nums []int) bool {
	h := &myHeap{} // 大顶堆

	for _, v := range nums {
				
    		// 根据条件，不一定每次都取到 d[0]=x-1, 所以要循环
        for h.Len()>0 {
            top := heap.Pop(h).([2]int)
            if top[0]==v { // 一样，重新起一组，说明d[0], 最小都 是=v了，想接在某个序列上是不可能了，只能是另起一段
                heap.Push(h, top)
                heap.Push(h, [2]int{v, 1})
                break
            } else if top[0]<v-1 { // 这一段已经无法接上了，要判断是不是超过3了
                if top[1]<3 {return false}
            } else { // top[0] == v-1 top[1]++, 以v结尾，并长度+1
                top[0]++
                top[1]++
                heap.Push(h, top)
                break
            }
        }
		
		if h.Len() == 0 {
			heap.Push(h, [2]int{v, 1})
			continue
		}
		
	}
	
	// 判断最终在堆里的序列长度是不是都超过
	for h.Len()>0 {
		top := heap.Pop(h).([2]int)
		if top[1]<3{return false}
	}
	
	return true
}

练习4 求第k大值

题目链接：力扣

题目大意

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

题目解析

构造一个小顶堆，容量是k, 遍历数组维护堆，始终保持堆内存储的是前k个最大值。

AC代码

type myHeap []int

func (h *myHeap) Less(i, j int) bool {
	return (*h)[i] < (*h)[j] // 小顶堆
}

func (h *myHeap) Swap(i, j int) {
	(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

func (h *myHeap) Len() int {
	return len(*h)
}

func (h *myHeap) Pop() (v interface{}) {
	*h, v = (*h)[:h.Len()-1], (*h)[h.Len()-1]
	return
}

func (h *myHeap) Push(v interface{}) {
	*h = append(*h, v.(int))
}

func findKthLargest(nums []int, k int) int {
	 h:= &myHeap{} // 堆中始终保持前k个最大
	 heap.Init(h)

	 for _, v:= range nums {
		 if h.Len()<k { // 不够k个直接加
		 	heap.Push(h, v)
		 } else if (*h)[0]<v { // 如果当前第k大小于v, 就替换掉
			heap.Pop(h)
			heap.Push(h, v)
		}
	 }
	 
	return heap.Pop(h).(int) // 堆顶既是第k大值
}

七、总结

主要内容：

  1. 堆是一种完全二叉树数据结构，可以使用数组表示。其性质是二叉对中的每个子树，根的值总是要比孩子的值要大（大顶堆）。
  2. 作用：1）堆排序；2) 快速选择最优值（最小，最大，条件最优等）3）取集合中前K大元素；4）通过定义多维条件，快速选择出最优解。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

八、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动用把刚才那4题A了。

  1. 排序应用 力扣
  2. 利用小顶堆解丑数：力扣
  3. 利用条件构造解决复杂问题：力扣
  4. 求第K大值: 力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

力扣 堆相关题目

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

poj

http://poj.org/problem?id=1442

以下将序号替换就是题目链接。

  1. 1442 -- Black Box
  2. 3614 -- Sunscreen
  3. 2387 -- Til the Cows Come Home
  4. 3253 -- Fence Repair
  5. 2010 -- Moo University - Financial Aid
  6. 2312 -- Battle City
  7. 2431 -- Expedition

hdu

http://acm.hdu.edu.cn/showproblem.php?pid=1242

以下将序号替换就是题目链接。

  1. http://acm.hdu.edu.cn/showproblem.php?pid=1242
  2. http://acm.hdu.edu.cn/showproblem.php?pid=4006
  3. http://acm.hdu.edu.cn/showproblem.php?pid=1873
  4. http://acm.hdu.edu.cn/showproblem.php?pid=1896
  5. http://acm.hdu.edu.cn/showproblem.php?pid=4546
  6. http://acm.hdu.edu.cn/showproblem.php?pid=1509

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。