AK F.*ing leetcode 流浪计划之前缀和

LightningBilly · 2021 年4 月 2 日 15:57

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

@[toc]

一、简介

在操作数组的算法中，前缀和算法是非常常见的，也非常高效的算法。

前缀和算法是利用dp思想，保存共用的前缀和结果，达到降低求区间和、求解特定条件区间等运算的复杂度。

前缀和算法（思想）在平时的算法中非常常用，操作比较简单，代码少，好理解，好实现，学习成本低。
前缀和基础作用是求解数组区间和。同时还可以结合hash, 堆等数据结构来求解选定条件下的区间。

差分是前缀和的衍生算法，利用差分思想能O(n)复杂度实现对数组作n次区间修改后查询数组结果。

在一维数组前缀和思想基础上，可以扩展到二维数组的情况。

前缀和是一种思想，不只适用于和，也可以用来运算积，二进制运算(异或、与、或)，求前缀最大（小）值等。

二、定义

原数组是arr[]。

前缀和的表现形式是一个数组preSum[]。

preSum[i] = arr[0]+arr[1]+…+arr[i]。

sum(i,j) = arr[i]+arr[i+1]+…+arr[j] , 从第i个元素到第j个元素之和。

利用preSum数组可以快速求解出sum(i,j)。

三、作用

求解区间和(积，异或等可逆运算)。
给定特定的条件求解区间或区间个数。
求解子矩阵和。
利用差分对数组区间修改，求解最终数组结果。
结合前缀和思想，求解前缀最大(小)值等数据，进而运算更复杂的问题。

四、数据定义及算法

数据定义

PreSum {
    preSum array // 数组 preSum[i]=arr[0]+arr[1]+...+arr[i]。
    // 常用有3种：
    InitPre(arr): // 初始化数据, 通过arr, 初始化preSum
    Sum(i,j)：// 查询区间和
    MaxSubArray() // 求解最大（小）子段和。
}

算法描述

具体可以看这个视频，讲得很详细。

https://www.bilibili.com/video/BV1pi4y1j7si?p=1

初始化preSum数组。

当i==0, preSum[0]=arr[i],

当i>0, preSum[i]=preSum[i-1]+arr[i]
求解Sum(i, j)

sum(i, j) = arr[i]+arr[i+1]+…+arr[j] = (arr[0]+arr[1]+…arr[i-1]+arr[i]+arr[i+1]+…+arr[j]) - (arr[0]+arr[1]+…arr[i-1]) = preSum[j] - preSum[i-1], 注意当i=0时，sum(i, j) = preSum[j]
MaxSubArray() 求解最大连续子段和

基本思路是：枚举每个以j为结尾的子段看哪个最优。

max(preSum[j]-preSum[x]) (x < j)

把上述公式优化一下得到 max(preSum[j]-preSum[x]) = preSum[j]-min(preSum[x]) (x < j)

这样只要保存前缀的最小值即可。

InitPre(arr): // 初始化数据
    preSum[0]=arr[0]
    for i <- 1 to n do
        preSum[i]<-preSum[i-1]+arr[i]

Sum(i,j)：// 查询区间和
    if i==0 : return preSum[j]
    return preSum[j]-preSum[i-1]

MaxSubArray(): // 查询最大子段和
    MinPre<-0
    best
    for i<-0 to n do
    	best <- preSum[i]-MinPre
    	MinPre <- min(MinPre, preSum[i])
    	
    return best

五、具体实现


func abs(a int) int {
	if a < 0 {
		return -a
	}
	return a
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

/*
前缀和
*/
type PreSum struct {
	preSum []int // 数组 preSum[i]=arr[0]+arr[1]+...+arr[i]。
}

// 常用有3种：
// 初始化数据, 通过arr, 初始化preSum
func (ps *PreSum) InitPre(arr []int) {
	ps.preSum = make([]int, len(arr))
	for i, v := range arr {
		if i == 0 {
			ps.preSum[0] = v
		} else {
			ps.preSum[i] = ps.preSum[i-1] + v
		}
	}
}

// 查询区间和
func (ps *PreSum) Sum(i, j int) int {
	if i <= 0 {
		return ps.preSum[j]
	}
	return ps.preSum[j] - ps.preSum[i-1]
}

//查询最大子段和
// 这里是普通情况，有时候有特殊要求，比如子段不能为空，子段有可能为负数==
func (ps *PreSum) MaxSubArray() int {
	minPre := 0
	best := 0

	for _, v := range ps.preSum {
		best = max(best, v-minPre)
		minPre = min(minPre, v)
	}

	return best
}

六、牛刀小试

练习1 最大子段和

题目链接力扣贪心，前缀和

题目大意

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [0]
输出：0
示例 4：

输入：nums = [-1]
输出：-1
示例 5：

输入：nums = [-100000]
输出：-100000

提示：

1 <= nums.length <= 3 * 10^4
-10^5 <= nums[i] <= 10^5

题目解析

根据贪心原理，枚举j, best = preSum[j] - min(preSum[x]) x<j

AC代码


func abs(a int) int {
	if a < 0 {
		return -a
	}
	return a
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

/*
前缀和
*/
type PreSum struct {
	preSum []int // 数组 preSum[i]=arr[0]+arr[1]+...+arr[i]。
}

// 常用有3种：
// 初始化数据, 通过arr, 初始化preSum
func (ps *PreSum) InitPre(arr []int) {
	ps.preSum = make([]int, len(arr))
	for i, v := range arr {
		if i == 0 {
			ps.preSum[0] = v
		} else {
			ps.preSum[i] = ps.preSum[i-1] + v
		}
	}
}

// 查询区间和
func (ps *PreSum) Sum(i, j int) int {
	if i <= 0 {
		return ps.preSum[j]
	}
	return ps.preSum[j] - ps.preSum[i-1]
}

//查询最大子段和
// 这里是普通情况，有时候有特殊要求，比如子段不能为空，子段有可能为负数==
func (ps *PreSum) MaxSubArray() int {
	minPre := 0
	best := ps.preSum[0] // 至少包含一个数字，以第1个数据为初始值，后续有更优的会更新

	for _, v := range ps.preSum {
		best = max(best, v-minPre)
		minPre = min(minPre, v)
	}

	return best
}

func maxSubArray(nums []int) int {
    ps := &PreSum{}
    ps.InitPre(nums)
    return ps.MaxSubArray()
}

练习2 前缀积应用

题目链接： 238. 除自身以外数组的乘积力扣前缀积(前缀和思想)

题目大意

给你一个长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]

提示：题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。

说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：
你可以在常数空间复杂度内完成这个题目吗？（出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

题目解析

output[i] = arr[0]*arr[1]*…*arr[i-1]*arr[i+1]*…*arr[n-1]

可以设置2个数组 prePro, backPro

prePro[i] = arr[0]*arr[1]*…*arr[i]

backPro[i] = arr[i]*arr[i+1]*…*arr[n-1]

output[i] = prePro[i-1] * backPro[i+1]

AC代码


func productExceptSelf(nums []int) []int {
	prePro, backPro := make([]int, len(nums)), make([]int, len(nums))

	for i, v := range nums {
		if i==0 {
			prePro[i]=v
			backPro[len(nums)-1-i]=nums[len(nums)-1-i]
		}else {
			prePro[i]=prePro[i-1]*v
			backPro[len(nums)-1-i]=nums[len(nums)-1-i]*backPro[len(nums)-1-i+1]
		}
	}

	for i:=0;i<len(nums);i++ {
		if i==0 {
			nums[i] = backPro[i+1]
		} else if i==len(nums)-1 {
			nums[i] = prePro[i-1]
		} else {
			nums[i] = prePro[i-1]*backPro[i+1]
		}
	}
	
	return nums
}

练习3 前缀最大值应用

题目链接：直方图的水量力扣前缀最大值(前缀和思想)

题目大意

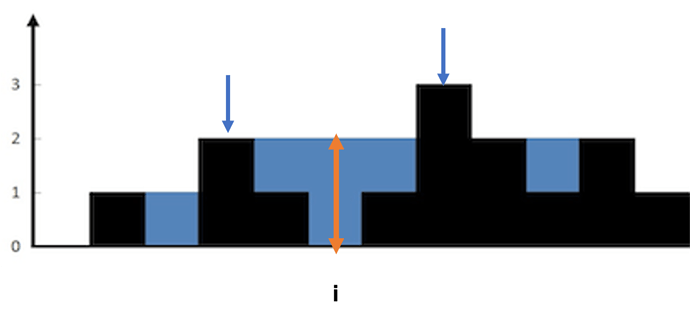
给定一个直方图(也称柱状图)，假设有人从上面源源不断地倒水，最后直方图能存多少水量?直方图的宽度为 1。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图，在这种情况下，可以接 6 个单位的水（蓝色部分表示水）。感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

题目解析

对于每个柱子的位置来说最高水平面肯定是固定的，那么是什么决定了水平面的高度呢，从图中可以看出，柱子I上的水平面是由2边最高的柱子(取2柱最低面)决定的。

那么我们就可以先求出每个柱子的左，右2边最高的地方然后再取最小值运算。

设置preMax[]，backMax[]

preMax[i]代表从0到i柱子最高的高度。

backMax[i]代表从i到len(height)-1柱子最高的高度。

第i根柱子上方的水量就是水平高度减去柱子高度 min(preMax[i-1], backMax[i+1]) -height[i] (当有水时，没水可能为负数，要特殊处理)

AC代码

func abs(a int) int {
	if a < 0 {
		return -a
	}
	return a
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func trap(height []int) int {
	preMax, backMax := make([]int, len(height)), make([]int, len(height))

	for i, v := range height { // 一次遍历计算出 preMax，通过坐标转化计算backMax
		if i==0 {
			preMax[i]=v
			backMax[len(height)-1-i]=height[len(height)-1-i] 
		}else {
			preMax[i]=max(preMax[i-1],v)
			backMax[len(height)-1-i]=max(height[len(height)-1-i], backMax[len(height)-1-i+1])
		}
	}
	
	sum :=0
	
	for i:=1 ;i<len(height)-1;i++ {
		sum += max(0, min(preMax[i-1], backMax[i+1]) - height[i]) // 小于0时要特殊处理
	}
	
	return sum
}

练习4 查询特定条件区间

题目链接： 560. 和为K的子数组力扣前缀和，哈希查询

题目大意

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :

数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。

题目解析

题意为求解 i,j 对数，使得sum(i,j) 区间和为k.
sum(i, j) = preSum[j]-preSum[i] = k
我们枚举 j, 然后去查询 preSum[i]= preSum[j]-k （i<j）即可。
可以设置一个hash map cnt[int]int
当遍历到一个preSum[i]时，cnt[preSum[i]]++.
这样可以快速查询到cnt[reSum[j]-k]

AC代码


func abs(a int) int {
	if a < 0 {
		return -a
	}
	return a
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

/*
前缀和
*/
type PreSum struct {
	preSum []int // 数组 preSum[i]=arr[0]+arr[1]+...+arr[i]。
}

// 常用有3种：
// 初始化数据, 通过arr, 初始化preSum
func (ps *PreSum) InitPre(arr []int) {
	ps.preSum = make([]int, len(arr))
	for i, v := range arr {
		if i == 0 {
			ps.preSum[0] = v
		} else {
			ps.preSum[i] = ps.preSum[i-1] + v
		}
	}
}

// 查询区间和
func (ps *PreSum) Sum(i, j int) int {
	if i <= 0 {
		return ps.preSum[j]
	}
	return ps.preSum[j] - ps.preSum[i-1]
}

//查询最大子段和
// 这里是普通情况，有时候有特殊要求，比如子段不能为空，子段有可能为负数==
func (ps *PreSum) MaxSubArray() int {
	minPre := 0
	best := ps.preSum[0] // 至少包含一个数字，以第1个数据为初始值，后续有更优的会更新

	for _, v := range ps.preSum {
		best = max(best, v-minPre)
		minPre = min(minPre, v)
	}

	return best
}

func subarraySum(nums []int, k int) int {
	cnt := map[int]int{0: 1} // 一开始前缀和为0的算1个
	ans := 0
	
	ps := &PreSum{}
	ps.InitPre(nums)
	for i := range nums {
		s := ps.preSum[i] - k
		ans += cnt[s] // 查询以当前数字为结尾之前有多少段满足条件
		cnt[ps.preSum[i]]++ // 前缀统计+1
	}

	return ans
}