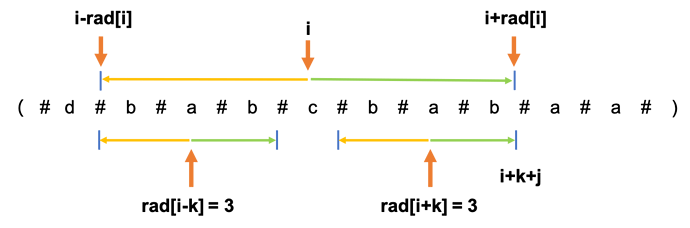AK F.*ing leetcode 流浪计划之回文串

[LightningBilly]

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

一、简介

“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。

其基本问题是判断是不是回文串以及判断子串是否为回文串。

在此基础上衍生出回文串计数，求最长回文子串，回文串构造，异型回文（需要对原串字符进行预处理或使用非常规判断规则）等问题。

此类题目的意思往往很容易理解，思路也很容易想到。但是如果没有掌握回文串基本问题的解法，往往是无法在规定时间内运行出结果。本文重点介绍O(n)复杂度下判断回文子串的算法。

对于判断回文串的方法，主要有单次判断和多次判断。

单次查询可以使用对撞指针法进行判断。多次查询的方法有双指针动态规划，中心扩展法，Manacher（马拉车）算法。

其中双指针动态规划，中心扩展法是O(n^2)的算法也比较好理解。Manacher算法需要做一些理论推导与证明，以便加深理解。

二、解题步骤

解题步骤

1. 将原串进行预处理(如有必要)
2. 计算子串是否为回文串
3. 根据题意选取回文子串
4. 进行回文计数，求最长回文串，回文构造等操作

三、作用

1. 查询最长回文子串
2. 统计回文子串
3. 构造回文子串
4. 判断回文串
5. 异型回文子串问题(比如对原串的字符进行相应的变化，对回文规则进行改变或加限制，将数字作为字符串)

四、经典算法介绍

单次查询可以使用对撞指针法进行判断。多次查询的方法有双指针动态规划，中心扩展法，Manacher（马拉车）算法。

其中双指针动态规划，中心扩展法是O(n^2)的算法也比较好理解。Manacher算法需要做一些理论推导与证明，以便加深理解。

判断一个串是否为回文串(单次查询)

主要思想是利用对撞指针判断断头尾是否相等，依次往中间靠拢，直到相遇。可以参考数组反转

普通情况

func isPalindrome(s string) bool {
	for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 { // 每判断完一个都往里移一个
		if s[i] != s[j] {return false}
	}
	return true
}

判断指定字符

func isNeedCheck(c byte) bool {
	
}

func isPalindromeSpecial(s string) bool {
	for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 { // 每判断完一个都往里移一个
		for ; i < j && !isNeedCheck(s[i]); i++ {} // 查找到第1个需要比较的元素
		for ; i < j && !isNeedCheck(s[j]); j-- {} // 查找最后一个需要比较的元素
		if s[i] != s[j] {return false}
	}
	return true
}

以上操作复杂都是O(n)对于单次查询的场景都可满足时间要求。

多次子串查询

极端情况下需求查询所有的子串。

	for i := 0; i < len(s); i++ { // 每判断完一个都往里移一个
		for j:=i;j<len(s);j++ {
			isPalindrome(s[i:j+1]) // 调用判断方法
		}
	}

以上算法的复杂是度O(n^3)，n的极限只能是100. 下面介绍2种O(n^2)的算法。

动态规划法O(n^2)

设dp[i\][j]为s[i:j+1]是否为回文串。

dp[i\][i] = true

dp[i\][j] = dp[i+1\][j-1] && s[i]==s[j] , 当2头相等并且中间是回文时，s[i:j+1]是回文，具体还有其他细节在代码中说明

通过以上转移方程先计算出所有子串的dp值，在判断时，直接访问即可。

func makeDp(s string) [][]bool {

	// 预申请内存
	dp := make([][]bool, len(s))
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]bool, len(s))
	}

	/*
		i,j 的循环值一定要注意。
		要保证在计算dp[i][j]时，dp[i+1][j-1]已经被计算过了。
		思考一下如果i从0开始会怎么样。？？？
	*/
	for i := len(s) - 1; i >= 0; i-- {
		for j := i; j < len(s); j++ {
			dp[i][j] = false //默认为false
			// 只有一个字符是回文
			if i == j {
				dp[i][j] = true
				continue
			}

			dp[i][j] = s[i] == s[j] && (i+1 >= j-1 || dp[i+1][j-1]) // i+1 >= j-1 时说明 s[i+1:j] 只有一个字符，或者空。
		}
	}
	return dp
}

以上计算 dp值是一个双重循环，总体复杂度是O(n^2), 后续判断子串的复杂度为O(1)总体复杂度是O(n^2)。对于规模n=1000左右的数据是适用的。

中心扩展法O(n^2)

• 算法过程介绍

指的是以某个字符为中心向2侧延伸，我们把一侧最长可延伸的字符个数(不包含中心字符)定义为’回文半径’。每个字符的回文半径形成了一个半径数组rad []。

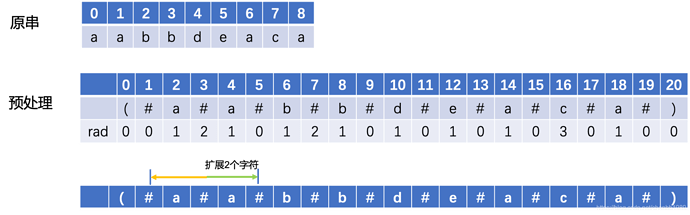
考虑到中心是2个字符的情况，我们对原字符串作一个特殊处理，先在字符中间和2端插入一个特殊字符’#’,在首尾加入字符’(’, ‘)’。然后按照单字符为中心来处理。

注意：前后一定要加入不同的字符

注意：前后一定要加入不同的字符

注意：前后一定要加入不同的字符

例如，原串s aabbdeaca ->s’ (#a#a#b#b#d#e#a#c#a#​)

如上图，rad[3]是由#向2边扩展，最多可以扩展2个字符，rad[2]=2。

仔细观察rad数组可以发现

当s’[i]是普通字符时，说明原串能以s[i/2-1]为中心向2边展开得到一个rad[i]长度的回文串。

当s’[i]=’#'时，说明原串能以s[(i-1)/2-1]s[(i+1)/2-1]两个字符为中心向2边延伸得到一个rad[i]长度的回文串。由于这里i肯定是奇数，所以(i+1)/2-1 = (i-1)/2，相当于是2个连续的字符。

举例，rad[2] = 1，我们可以得到a 是一个长度为1的回文串。

rad[3]=2 ,我们可以得到aa 是一个长度为2的回文串。

rad[16]=3 ,我们可以得到aca 是一个长度为3的回文串。

为什么会有这个性质，我的个人理解是这样。这是因为我们加入的字符都是#号当一个字母对应上后，扩展时会自然会带上一个#号。所以半径就是回文串的长度。

• 如何解决常规问题(求最长回文子串和判断回文子串)

1 对于求最长回文子串，由于rad是存储的以某个字符向外延伸的最长回文子串，只要遍历rad就可以得到最大值。

2 判断回文子串s[i:j+1]

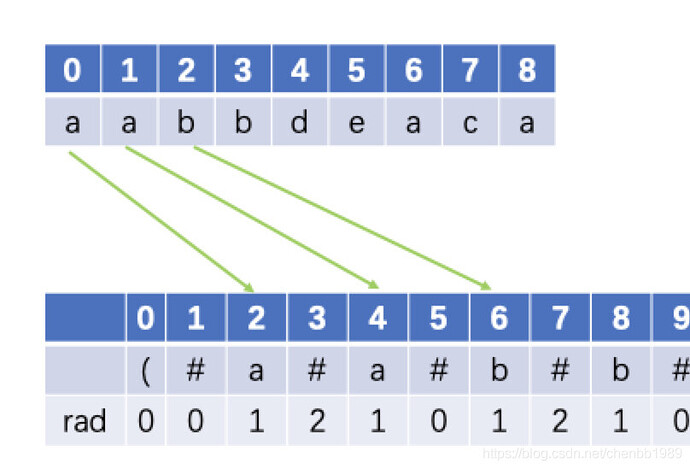
看了解一下原串与新的下标对应关系，从图中可以看出 原串中的i对应到新串的2*i+2

判断子串 i到j 是不是回文串，只要找到新串的中心x，查看rad[x]>=j-i+1. x = ((2*i+2) + (2*j+2))/2 = i+j+2

type Palindrome struct {
	rad []int
	arr []byte
	s string
}

func (p *Palindrome)Init(s string) {
	p.s=s
	p.makeRad(s)
}

func (p *Palindrome)makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3]= byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for i:=1;i<len(arr)-1 ;i++  {
		for ;arr[i-1-rad[i]]==arr[i+1+rad[i]];rad[i]++{}
	}
	p.rad = rad
	//fmt.Println(rad)
}

// 检查s[i:j+1]是不是回文
func (p *Palindrome)Check(i, j int) bool {
	// 原来的i对应到新数组的i*2+2, 新数组中心点是(i*2+2 + j*2+2)/2 = i+j+2
	// 要判断半径是不是>= j-i+1
	mid := i+j+2
	return p.rad[mid]>=j-i+1
}

在上面代码中，求rad是双重循环，复杂度O(n^2)

Manacher(马拉车算法) O(n)

Manacher算法是在上面中心扩展算法的基础上，优化rad生成过程，从而得到O(n)复杂度。

• 过程介绍

基本框架与中心扩展法一样，我们主要介绍计算半径的优化。

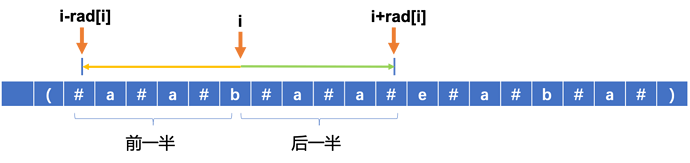
以b向外延伸，把这个延伸分成前一半和后一半

由回文性质可以知前一半和后一半是对称的。

由于我们rad[i]是从小到大计算的，当计算rad[i]时, x<i 的 rad[x]已经计算完毕，可以想办法把这部分信息用上。

那如果知道前一半里的某个rad[x] (i-rad[i]<=x<i),

是不是可以推测出后一半rad[j] (i<j<=i+rad[i])

大致可以分成3种情况：

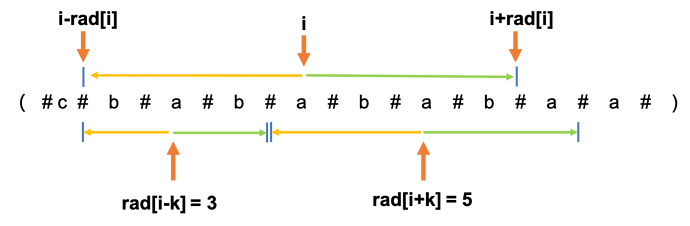
• 情况1 (i-rad[i]<i-k-rad[i-k] 可以直接赋值)

上图中i-rad[i]<i-k-rad[i-k], 相当于i-k 的扩展区域在rad[i]的管辖区域内，根据对称性，i+k的扩展区域也应该在rad[i]的管辖区域。所以rad[i+k]=rad[i-k]

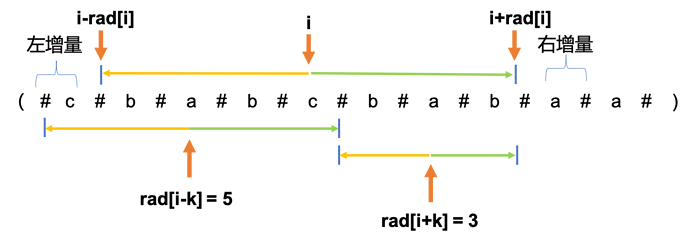
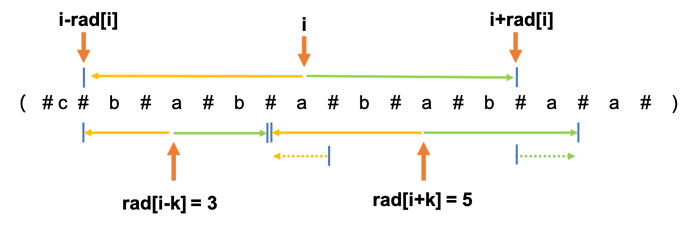
• 情况2 (i-rad[i]=i-k-rad[i-k] 无法确定)

上图看出i-rad[i]=i-k-rad[i-k] 时，有可能存在右边边缘可以继续扩展的情况，这是rad[i]无法管辖的，所以无法进行直接赋值。

• 情况3 (i-rad[i]>i-k-rad[i-k] 可以确定)

上图展示了i-rad[i]>i-k-rad[i-k]情况下，rad[i+k]的取值情况。

左增量，右增量是超出rad[i]的管辖，同时说明左增量与右增量不是对称的。(反证，如果是的话，rad[i]肯定要增加)

由于rad[i-k]=5, 说明左边以a为中心最多可以向2边扩展5个字符，说明可以以a（下标i-k）为中心扩展 i-k - i-rad[i] = rad[i]-k个字符，对称到右边就是以a(下标i+k)为中心扩展 i+rad[i] - (i+k) = rad[i]-k 个字符

所以，右增量不能作为i+k字符的扩展范围，rad[i+k] 最多只能扩展到i+rad[i]。rad[i+k]=rad[i]-k。

结合以上3种情况，在i-rad[i]!=i-k-rad[i-k]的情况下，rad[i+k]可以直接确定，rad[i+k] = min(rad[i]-k, rad[i-k])

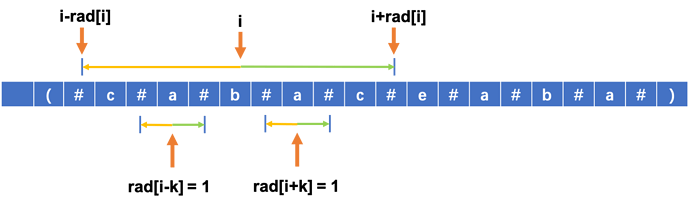
当i-rad[i]=i-k-rad[i-k]时，还要继续往外扩展。但是此时不用从0开始，可以直接从rad[i+k]=3开始（虚线部分）。

• rad计算代码

func (p *Palindrome) makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3] = byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for k, j, i := 0, 0, 1; i < len(arr)-1; i += k {
		for ; arr[i-1-j] == arr[i+1+j]; j++ {}
		rad[i] = j // 通过扩展得到当前字符回文半径
		//for k=1; k <= rad[i] && i-rad[i]!=i-k-rad[i-k]; k++ { // 通过移项可以得到下面简化条件
		for k = 1; k <= j && rad[i-k] != rad[i]-k; k++ {
			rad[i+k] = min(rad[i-k], rad[i]-k)
		}
		/*
			rad[i]=j
			上面退出循环2种情况
			1. k>rad[i], 说明k>j ==> j=0
			2. rad[i-k]==rad[i]-k ==> j=j-k
		*/
		j = max(0, j-k) // j可以继续前面已经扩展的结果。
	}
	p.rad = rad
	//fmt.Println(rad)
}

上述代码的复杂度是O(n)

主要分析一下计算半径部分。

i+rad[i] 代表的是从i向外延伸的最右边界

当一个大循环结束后，有2种情况。

k>rad[i]时，j=0, i+k+j = i+rad[i]+1 > i+rad[i]

k<=rad[i]时, j=rad[i]-k, i+k+j = i+rad[i] .

说明， i+k+j 整体是一直是增大的且i+k+j<len(arr) 。

所以总体复杂度是O(n)。

• 整体代码

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

type Palindrome struct {
	rad []int
	arr []byte
	s   string
}

func (p *Palindrome) Init(s string) {
	p.s = s
	p.makeRad(s)
}

func (p *Palindrome) makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3] = byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for k, j, i := 0, 0, 1; i < len(arr)-1; i += k {
		for ; arr[i-1-j] == arr[i+1+j]; j++ {}
		rad[i] = j // 通过扩展得到当前字符回文半径
		//for k=1; k <= rad[i] && i-rad[i]!=i-k-rad[i-k]; k++ { // 通过移项可以得到下面简化条件
		for k = 1; k <= j && rad[i-k] != rad[i]-k; k++ {
			rad[i+k] = min(rad[i-k], rad[i]-k)
		}
		/*
			rad[i]=j
			上面退出循环2种情况
			1. k>rad[i], 说明k>j ==> j=0
			2. rad[i-k]==rad[i]-k ==> j=j-k
		*/
		j = max(0, j-k) // j可以继承前面已经扩展的结果。
	}
	p.rad = rad
	//fmt.Println(rad)
}

// 检查s[i:j+1]是不是回文
func (p *Palindrome) Check(i, j int) bool {
	// 原来的i对应到新数组的i*2+2, 新数组中心点是(i*2+2 + j*2+2)/2 = i+j+2
	// 要判断半径是不是>= j-i+1
	mid := i + j + 2
	return p.rad[mid] >= j-i+1
}

五、牛刀小试

练习1 最长回文子串

题目链接 https://leetcode-cn.com/problems/longest-palindromic-substring/

题目大意

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。
示例 2：

输入：s = “cbbd”
输出：“bb”
示例 3：

输入：s = “a”
输出：“a”
示例 4：

输入：s = “ac”
输出：“a”

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母（大写和/或小写）组成

题目解析

题目数据范围是1000，枚举判断，动态规划，中心扩展，Manacher都可用。

枚举判断：枚举所有子串判断是否为回文子串，取最优。

动态规划：直接枚举子串，判断是否为回文串，取最长。

中心扩展：枚举中心，往外扩展，取最长子串。

Manacher：找到最长半径，然后去构造出子原串

AC代码

• 枚举判断

func isPalindrome(s string) bool {
	for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 { // 每判断完一个都往里移一个
		if s[i] != s[j] {return false}
	}
	return true
}

func longestPalindrome(s string) string {
	res := ""
	
	for i:=0;i<len(s);i++ {
		for j:=i;j<len(s);j++ {
			if isPalindrome(s[i:j+1]) && j-i+1>len(res){res = s[i:j+1]}
		}
	}
	
	return res
}

• 动态规划

func makeDp(s string) [][]bool {

	// 预申请内存
	dp := make([][]bool, len(s))
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]bool, len(s))
	}

	/*
		i,j 的循环值一定要注意。
		要保证在计算dp[i][j]时，dp[i+1][j-1]已经被计算过了。
		思考一下如果i从0开始会怎么样。？？？
	*/
	for i := len(s) - 1; i >= 0; i-- {
		for j := i; j < len(s); j++ {
			dp[i][j] = false //默认为false
			// 只有一个字符是回文
			if i == j {
				dp[i][j] = true
				continue
			}

			dp[i][j] = s[i] == s[j] && (i+1 >= j-1 || dp[i+1][j-1]) // i+1 >= j-1 时说明 s[i+1:j] 只有一个字符，或者空。
		}
	}
	return dp
}

func longestPalindrome(s string) string {
	res := ""
	dp := makeDp(s)

	for i:=0;i<len(s);i++ {
		for j:=i;j<len(s);j++ {
			if dp[i][j] && j-i+1>len(res){res = s[i:j+1]}
		}
	}

	return res
}

• Manacher法

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

type Palindrome struct {
	rad []int
	arr []byte
	s   string
}

func (p *Palindrome) Init(s string) {
	p.s = s
	p.makeRad(s)
}

func (p *Palindrome) makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3] = byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for k, j, i := 0, 0, 1; i < len(arr)-1; i += k {
		for ; arr[i-1-j] == arr[i+1+j]; j++ {}
		rad[i] = j // 通过扩展得到当前字符回文半径
		//for k=1; k <= rad[i] && i-rad[i]!=i-k-rad[i-k]; k++ { // 通过移项可以得到下面简化条件
		for k = 1; k <= j && rad[i-k] != rad[i]-k; k++ {
			rad[i+k] = min(rad[i-k], rad[i]-k)
		}
		/*
			rad[i]=j
			上面退出循环2种情况
			1. k>rad[i], 说明k>j ==> j=0
			2. rad[i-k]==rad[i]-k ==> j=j-k
		*/
		j = max(0, j-k) // j可以继续前面已经扩展的结果。
	}
	p.rad = rad
	//fmt.Println(rad)
}

// 检查s[i:j+1]是不是回文
func (p *Palindrome) Check(i, j int) bool {
	// 原来的i对应到新数组的i*2+2, 新数组中心点是(i*2+2 + j*2+2)/2 = i+j+2
	// 要判断半径是不是>= j-i+1
	mid := i + j + 2
	return p.rad[mid] >= j-i+1
}

// 获取最长，去除所有#号即可
func (p *Palindrome) GetLongest() (string, int) {
	res := ""
	l :=0
	for i:=1;i<len(p.rad)-1;i++ {
		if p.rad[i]>l {
			l = p.rad[i]
			res = string(p.arr[i-l:i+l+1])
		}
	}
	
	return strings.Replace(res, "#", "", -1), l
}


func longestPalindrome(s string) string {

	p := &Palindrome{}
	p.Init(s)
	res,_ :=p.GetLongest() 
	return res
}

练习2 验证回文串

题目链接：力扣

题目大意

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明：本题中，我们将空字符串定义为有效的回文串。

示例 1:

输入: “A man, a plan, a canal: Panama”
输出: true
示例 2:

输入: “race a car”
输出: false

题目解析

先把大写转成小写，调用指定字符模板

AC代码

func isNeedCheck(c byte) bool {
	return ('a'<=c&& c<='z') || ('0'<=c && c<='9')
}

func isPalindromeSpecial(s string) bool {
	for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 { // 每判断完一个都往里移一个
		for ; i < j && !isNeedCheck(s[i]); i++ {} // 查找到第1个需要比较的元素
		for ; i < j && !isNeedCheck(s[j]); j-- {} // 查找最后一个需要比较的元素
		if s[i] != s[j] {return false}
	}
	return true
}

func isPalindrome(s string) bool {
	return isPalindromeSpecial(strings.ToLower(s))
}

练习3 构建回文串检测

题目链接：力扣

题目大意

给你一个字符串 s，请你对 s 的子串进行检测。

每次检测，待检子串都可以表示为 queries[i] = [left, right, k]。我们可以 重新排列 子串 s[left], …, s[right]，并从中选择 最多 k 项替换成任何小写英文字母。

如果在上述检测过程中，子串可以变成回文形式的字符串，那么检测结果为 true，否则结果为 false。

返回答案数组 answer[]，其中 answer[i] 是第 i 个待检子串 queries[i] 的检测结果。

注意：在替换时，子串中的每个字母都必须作为 独立的 项进行计数，也就是说，如果 s[left…right] = “aaa” 且 k = 2，我们只能替换其中的两个字母。（另外，任何检测都不会修改原始字符串 s，可以认为每次检测都是独立的）

示例：

输入：s = “abcda”, queries = [[3,3,0],[1,2,0],[0,3,1],[0,3,2],[0,4,1]]
输出：[true,false,false,true,true]
解释：
queries[0] : 子串 = “d”，回文。
queries[1] : 子串 = “bc”，不是回文。
queries[2] : 子串 = “abcd”，只替换 1 个字符是变不成回文串的。
queries[3] : 子串 = “abcd”，可以变成回文的 “abba”。 也可以变成 “baab”，先重新排序变成 “bacd”，然后把 “cd” 替换为 “ab”。
queries[4] : 子串 = “abcda”，可以变成回文的 “abcba”。

提示：

1 <= s.length, queries.length <= 10^5
0 <= queries[i][0] <= queries[i][1] < s.length
0 <= queries[i][2] <= s.length
s 中只有小写英文字母

题目解析

根据题意，本质是给一个字符串问能不能变化k个字符，并且可以重排得到一个回文串。

由于可以重排，所以只跟每种字母个数相关。

比如，abcda ，a(2), b(1), c(1), d(1)根据贪心原理，回文串最多只能有1种字母是奇数个。所以需要对奇数个进行统计s，然后改变s/2个。

现在题目有多个查询。相当于是查询区间里各字母的个数。

可以使用preSum思想

preSum[a][i]代表从0到第i个 位置为止，a出现的次数。

那么从i到j, a 出现的次数就是preSum[a][j] - preSum[a][i-1] O(1)

总体复杂度O(26*n)

AC代码

func getCnt(s string) [26][]int {
	cnt := [26][]int{}
	for i := 0; i < 26; i++ {
		cnt[i] = make([]int, len(s)+1)
	}

	for key, value := range s {
		for i := int32(0); i < 26; i++ {
			cnt[i][key+1] = cnt[i][key]
			if value-'a' == i {
				cnt[i][key+1]++
			}
		}
	}

	return cnt
}

func canMakePaliQueries(s string, queries [][]int) []bool {
	cnt :=getCnt(s)
	ans := make([]bool, len(queries))
	for i, q := range queries {
		total :=0
		for j:=0;j<26;j++ {
			total += (cnt[j][q[1]+1]-cnt[j][q[0]])&1 // 判断奇数
		}
		ans[i]=q[2]>=total /2
	}
	
	return ans
}

练习4 回文素数

题目链接：力扣

题目大意

求出大于或等于 N 的最小回文素数。

回顾一下，如果一个数大于 1，且其因数只有 1 和它自身，那么这个数是素数。

例如，2，3，5，7，11 以及 13 是素数。

回顾一下，如果一个数从左往右读与从右往左读是一样的，那么这个数是回文数。

例如，12321 是回文数。

示例 1：

输入：6
输出：7
示例 2：

输入：8
输出：11
示例 3：

输入：13
输出：101

提示：

1 <= N <= 10^8
答案肯定存在，且小于 2 * 10^8。

题目解析

答案肯定是在 2*10^8 相当于最多只有9位数，我们可以先去构造前缀，然后利用前缀构造出整数。

构造出整数后再去判断是不是素数。

枚举时要先考虑短位数，再考虑中间位增加。

复杂度10^5 * sqrt(n)

AC代码

func isP(n int) bool {
    if n<4{return true}
	for i := 2; i <= int(math.Sqrt(float64(n)))+1; i++ {
		//for i := 2; i <= n-1; i++ {
		if n%i == 0 {
			return false
		}
	}
	return true
}

func getPalinNum(n int, mid int) int {
	ans := n
	if mid >= 0 {
		ans = ans*10 + mid
	}
	for ; n > 0; n /= 10 {
		ans = ans*10 + n%10
	}

	return ans
}

func primePalindrome(N int) int {
    // 只有一位特殊判断
	for i := 2; i < 10; i++ {
		if i < N {
			continue
		}
		if isP(i) {
			return i
		}
	}
    // 枚举前缀长度
	for l := 1; l < 5; l++ {
		low, up := int(math.Pow10(l-1)), int(math.Pow10(l))
        // 枚举偶数位
		for i := low; i < up; i++ {
			n := getPalinNum(i, -1)
			if n < N {
				continue
			}
			if isP(n) {
				return n
			}
		}

        // 枚举奇数位
		for i := low; i < up; i++ {
            // 中间位从小到大
			for mid := 0; mid <= 9; mid++ {

				n := getPalinNum(i, mid)
				if n < N {
					continue
				}
				if isP(n) {
					return n
				}
			}
		}
	}

	return 0
}

六、代码模板

• 动态规划

func makeDp(s string) [][]bool {

	// 预申请内存
	dp := make([][]bool, len(s))
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]bool, len(s))
	}

	/*
		i,j 的循环值一定要注意。
		要保证在计算dp[i][j]时，dp[i+1][j-1]已经被计算过了。
		思考一下如果i从0开始会怎么样。？？？
	*/
	for i := len(s) - 1; i >= 0; i-- {
		for j := i; j < len(s); j++ {
			dp[i][j] = false //默认为false
			// 只有一个字符是回文
			if i == j {
				dp[i][j] = true
				continue
			}

			dp[i][j] = s[i] == s[j] && (i+1 >= j-1 || dp[i+1][j-1]) // i+1 >= j-1 时说明 s[i+1:j] 只有一个字符，或者空。
		}
	}
	return dp
}

• 中心扩展法

type Palindrome struct {
	rad []int
	arr []byte
	s string
}

func (p *Palindrome)Init(s string) {
	p.s=s
	p.makeRad(s)
}

func (p *Palindrome)makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3]= byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for i:=1;i<len(arr)-1 ;i++  {
		for ;arr[i-1-rad[i]]==arr[i+1+rad[i]];rad[i]++{}
	}
	p.rad = rad
	//fmt.Println(rad)
}

// 检查s[i:j+1]是不是回文
func (p *Palindrome)Check(i, j int) bool {
	// 原来的i对应到新数组的i*2+2, 新数组中心点是(i*2+2 + j*2+2)/2 = i+j+2
	// 要判断半径是不是>= j-i+1
	mid := i+j+2
	return p.rad[mid]>=j-i+1
}

• Manacher

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

type Palindrome struct {
	rad []int
	arr []byte
	s   string
}

func (p *Palindrome) Init(s string) {
	p.s = s
	p.makeRad(s)
}

func (p *Palindrome) makeRad(s string) {
	arr := make([]byte, len(s)*2+3)
	// 构造新数组
	arr[0], arr[1], arr[len(arr)-1] = '(', '#', ')'
	for i, v := range s {
		arr[i*2+2], arr[i*2+3] = byte(v), '#'
	}
	p.arr = arr
	//fmt.Println(string(arr))

	rad := make([]int, len(arr))
	// 计算半径
	for k, j, i := 0, 0, 1; i < len(arr)-1; i += k {
		for ; arr[i-1-j] == arr[i+1+j]; j++ {}
		rad[i] = j // 通过扩展得到当前字符回文半径
		//for k=1; k <= rad[i] && i-rad[i]!=i-k-rad[i-k]; k++ { // 通过移项可以得到下面简化条件
		for k = 1; k <= j && rad[i-k] != rad[i]-k; k++ {
			rad[i+k] = min(rad[i-k], rad[i]-k)
		}
		/*
			rad[i]=j
			上面退出循环2种情况
			1. k>rad[i], 说明k>j ==> j=0
			2. rad[i-k]==rad[i]-k ==> j=j-k
		*/
		j = max(0, j-k) // j可以继续前面已经扩展的结果。
	}
	p.rad = rad
	//fmt.Println(rad)
}

// 检查s[i:j+1]是不是回文
func (p *Palindrome) Check(i, j int) bool {
	// 原来的i对应到新数组的i*2+2, 新数组中心点是(i*2+2 + j*2+2)/2 = i+j+2
	// 要判断半径是不是>= j-i+1
	mid := i + j + 2
	return p.rad[mid] >= j-i+1
}

动态规划法代码比较少，逻辑简单，现场写起来比较快。

Manercher代码多些，复杂度优。解决问题能力更强。

七、总结

主要内容：

1. 回文串问题出现非常频繁，掌握相关算法对解题非常有帮助。
2. 介绍回文串相关算法的作用
3. 介绍回文串相关的常用算法，其中动态规划和Manacher要重点理解。

回文串判断是回文问题中最基础的问题，构造回文也是经常遇到的题目。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode）。给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

八、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动用把刚才那4题A了。

1. 最长回文子串 题目链接 力扣
2. 验证回文串 题目链接 力扣
3. 构建回文串检测 题目链接 力扣
4. 回文素数 题目链接 力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

5. 最长回文子串 https://leetcode-cn.com/problems/longest-palindromic-substring/ 扩展法 manacher dp

9. 回文数 https://leetcode-cn.com/problems/palindrome-number/ 转数组 判断

125. 验证回文串 https://leetcode-cn.com/problems/valid-palindrome/ 查找特殊字符 验证字符串

131. 分割回文串 https://leetcode-cn.com/problems/palindrome-partitioning/ 回文串 dp 枚举 dfs

132. 分割回文串 II https://leetcode-cn.com/problems/palindrome-partitioning-ii/ dp 枚举 回文串

214. 最短回文串 https://leetcode-cn.com/problems/shortest-palindrome/ 马拉车 枚举 贪心

234. 回文链表 https://leetcode-cn.com/problems/palindrome-linked-list/ 模拟 反转

336. 回文对 https://leetcode-cn.com/problems/palindrome-pairs/ 贪心 字符串查询

409. 最长回文串 https://leetcode-cn.com/problems/longest-palindrome/ 扩展法 manacher dp

479. 最大回文数乘积 https://leetcode-cn.com/problems/largest-palindrome-product/ 枚举 模拟

516. 最长回文子序列 https://leetcode-cn.com/problems/longest-palindromic-subsequence/ dp

564. 寻找最近的回文数 https://leetcode-cn.com/problems/find-the-closest-palindrome/ 贪心 构造

647. 回文子串 https://leetcode-cn.com/problems/palindromic-substrings/ 扩展法 manacher dp

680. 验证回文字符串 Ⅱ https://leetcode-cn.com/problems/valid-palindrome-ii/ 贪心 双指针

730. 统计不同回文子序列 https://leetcode-cn.com/problems/count-different-palindromic-subsequences/ 枚举 dp(判断)

866. 回文素数 https://leetcode-cn.com/problems/prime-palindrome/ 素数 回文判断

906. 超级回文数 https://leetcode-cn.com/problems/super-palindromes/ 构造

1147. 段式回文 https://leetcode-cn.com/problems/longest-chunked-palindrome-decomposition/ dp kmp

1177. 构建回文串检测 https://leetcode-cn.com/problems/can-make-palindrome-from-substring/ 贪心 区间求和

1278. 分割回文串 III https://leetcode-cn.com/problems/palindrome-partitioning-iii/ dp 模拟

1312. 让字符串成为回文串的最少插入次数 https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/ dp 模拟

1328. 破坏回文串 https://leetcode-cn.com/problems/break-a-palindrome/ 贪心 模拟

1332. 删除回文子序列 https://leetcode-cn.com/problems/remove-palindromic-subsequences

1400. 构造 K 个回文字符串 https://leetcode-cn.com/problems/construct-k-palindrome-strings/ hash 贪心

1457. 二叉树中的伪回文路径 https://leetcode-cn.com/problems/pseudo-palindromic-paths-in-a-binary-tree/ dfs hash 贪心

1616. 分割两个字符串得到回文串 https://leetcode-cn.com/problems/split-two-strings-to-make-palindrome/ 贪心

1745. 回文串分割 IV https://leetcode-cn.com/problems/palindrome-partitioning-iv/ 回文判断 枚举

面试题 01.04. 回文排列 https://leetcode-cn.com/problems/palindrome-permutation-lcci/ hash 贪心

面试题 02.06. 回文链表 https://leetcode-cn.com/problems/palindrome-linked-list-lcci/ 链表 模拟

---

以上题目太多，大家适当选择就行，下面还有进阶题目。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

poj

http://poj.org/problem?id=1159 动态规划

hdu

http://acm.hdu.edu.cn/showproblem.php?pid=1597

以下将序号替换就是题目链接。

http://acm.hdu.edu.cn/showproblem.php?pid=3294 模拟，manacher算法

http://acm.hdu.edu.cn/showproblem.php?pid=3068 manacher算法

http://acm.hdu.edu.cn/showproblem.php?pid=4513 manacher算法

http://acm.hdu.edu.cn/showproblem.php?pid=3948 manacher算法

http://acm.hdu.edu.cn/showproblem.php?pid=1431 枚举

http://acm.hdu.edu.cn/showproblem.php?pid=4632

http://acm.hdu.edu.cn/showproblem.php?pid=6156

zoj

https://vjudge.net/problem/ZOJ-3661 manacher 前缀和

hihocoder

最长回文子串 http://hihocoder.com/problemset/problem/1032

回文字符序列 http://hihocoder.com/problemset/problem/1149

回文字符串 http://hihocoder.com/problemset/problem/1323

回文子串的数量 http://hihocoder.com/problemset/problem/1589

本质不同的回文子串的数量 http://hihocoder.com/problemset/problem/1602

回文字符串2 http://hihocoder.com/problemset/problem/1721

偶数长度回文子串 http://hihocoder.com/problemset/problem/1788

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。