1579 - 保证图可完全遍历 - 最小生成树 - 并查集 - 贪心 - 数学分析

算法之美
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

[toc]

题目描述

[1579] 保证图可完全遍历

https://leetcode-cn.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3 种类型的边：

类型 1：只能由 Alice 遍历。
类型 2：只能由 Bob 遍历。
类型 3：Alice 和 Bob 都可以遍历。
给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

示例 1：

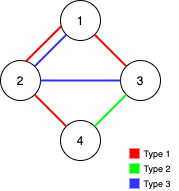
在这里插入图片描述

输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2：

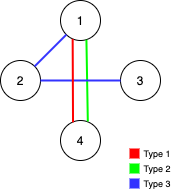
在这里插入图片描述

输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3：

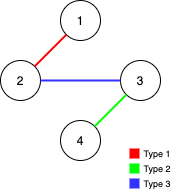
在这里插入图片描述

输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

提示：

1 <= n <= 10^5
1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
edges[i].length == 3
1 <= edges[i\][0] <= 3
1 <= edges[i\][1] < edges[i\][2] <= n
所有元组 (typei, ui, vi) 互不相同

Related Topics
  • 最小生成树
  • 贪心
  • 数学分析

    • 题目剖析&信息挖掘

    此题考查最小生成树特性的应用。

    具体实现用到了并查集 并查集学习资料

    解题思路

    方法一 模拟+贪心+数学

    分析

    由图论可知一个n结点无向连通图至少要n-1条边

    假设最优情况下，类型1选择了 x条，类型2选择了y 条，类型3选择了z条

    x+z=n-1 （1）

    y+z=n-1 （2）

    图上说要删除最多的边

    那其实就是要求x+y+z最小。

    对1，2式相加并移项

    x+y+z=2n-2-z

    从上式可以看出 z大越大越好，也就是类型3的边越多越好。

    所以，结论就是先把类型3的边用了，再用1，2.

    • 疑问1 有没有可能先用类型3的边然后导致构造不出连通图。

    答：先选择3，可以认为在原来1，2的基础上增加了一些边（这种情况只会增加连通的可能性）。根据最小生成树原理，在权值相同的情况下，选择的顺序是不影响连通性的。

    • 疑问2 有没有可能选择了类型3中的某条边，会导致最终结果不是最优的。

    答：结论是不会。假设alice, bob现在都已经连通了，也就是他们都选择了 x=n-1, y=n-1, 现在有一条3边过来，

    加入到alice, bob以后必然会产生环，所以必然可以拿走一条原来的边。相当于只要类型3选择一条，就可以拿走1，2各一条。从公式也可以反应出来。

    思路

    
func maxNumEdgesToRemove(n int, edges [][]int) int {
	// 排序，把类型为3的排到最前面

	usAlice, usBob := &UnionFindSet{}, &UnionFindSet{} // 初始化alice 和bob的并查集
	usAlice.InitUnionSet(n + 1)                        // 编号从1开始的
	usBob.InitUnionSet(n + 1)

	sum := 0 // 去除的边
	for _, edge := range edges {
		switch edge[0] {
		case 3:
			if !usAlice.UnionV2(edge[1], edge[2]) { // 加不上, 删除一条边
				sum++
			}
			usBob.UnionV2(edge[1], edge[2]) // bob同步加上

		case 2:
			// 往bob上加
			if !usBob.UnionV2(edge[1], edge[2]) { // 加不上删除一条
				sum++
			}
		case 1:
			// 往alice上加
			if !usAlice.UnionV2(edge[1], edge[2]) { // 加不上删除一条
				sum++
			}
		}
	}

	// 判断是不是都连通了
	if !isLinked(usAlice, n) || !isLinked(usBob, n) {
		// 至少有一个未连通
		return -1
	}

	return sum
}

    注意

    • 不连通情况下优先返回-1。
    • 考虑n=1的情况。
    • 类型3的边只算一条边。

    知识点

    • 最小生成树
    • 贪心
    • 数学分析

    复杂度

    • 时间复杂度：O(edges)
    • 空间复杂度：O(n+edges)

    参考

    并查集学习资料

    代码实现

    
/*
并查集，判连通用
*/
type UnionFindSet struct {
	father  []int // 存储结点的父亲
	height  []int // 存储结点的父亲
	nodeNum int   // 总结点个数
}

func (us *UnionFindSet) InitUnionSet(n int) {
	us.nodeNum = n + 1 // 不加也可以，有人喜欢以0开头
	us.father = make([]int, us.nodeNum)
	us.height = make([]int, us.nodeNum)
	for i, _ := range us.father {
		us.father[i] = i
		us.height[i] = 1
	}
}

func (us *UnionFindSet) FindV2(x int) int {
	root := x // 保存好路径上的头结点
	for us.father[root] != root {
		root = us.father[root]
	}
	/*
		从头结点开始一直往根上遍历
		把所有结点的father直接指向root。
	*/
	for us.father[x] != x {
		// 一定要先保存好下一个结点，下一步是要对us.father[x]进行赋值
		temp := us.father[x]
		us.father[x] = root
		x = temp
	}

	return root
}

/*
需要加入height[]属性，初始化为1.
*/
//合并结点
func (us *UnionFindSet) UnionV2(x, y int) bool {
	x = us.FindV2(x)
	y = us.FindV2(y)
	if x == y {
		return false
	}
	if us.height[x] < us.height[y] {
		us.father[x] = y
	} else if us.height[x] > us.height[y] {
		us.father[y] = x
	} else {
		us.father[x] = y
		us.height[y]++
	}
	return true
}

func isLinked(us *UnionFindSet, n int) bool {
	rootNum :=0
	for i:=1;i<=n;i++ {
		if us.FindV2(i)==i{
			rootNum++
		}
	}

	return rootNum==1
}

func maxNumEdgesToRemove(n int, edges [][]int) int {
	// 排序，把类型为3的排到最前面
	sort.Slice(edges, func(i, j int) bool {
		return edges[i][0] > edges[j][0]
	})

	usAlice, usBob := &UnionFindSet{}, &UnionFindSet{} // 初始化alice 和bob的并查集
	usAlice.InitUnionSet(n + 1)                        // 编号从1开始的
	usBob.InitUnionSet(n + 1)

	sum := 0 // 去除的边
	for _, edge := range edges {
		switch edge[0] {
		case 3:
			if !usAlice.UnionV2(edge[1], edge[2]) { // 加不上, 删除一条边
				sum++
			}
			usBob.UnionV2(edge[1], edge[2]) // bob同步加上

		case 2:
			// 往bob上加
			if !usBob.UnionV2(edge[1], edge[2]) { // 加不上删除一条
				sum++
			}
		case 1:
			// 往alice上加
			if !usAlice.UnionV2(edge[1], edge[2]) { // 加不上删除一条
				sum++
			}
		}
	}

	// 判断是不是都连通了
	if !isLinked(usAlice, n) || !isLinked(usBob, n) {
		// 至少有一个未连通
		return -1
	}

	return sum
}

    相关题目

    并查集学习资料 这里整理了资料

    本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。
    在这里插入图片描述