欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
题目描述
[1738] 找出第 K 大的异或坐标值
给你一个二维矩阵 matrix 和一个整数 k ,矩阵大小为 m x n 由非负整数组成。
矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j](下标从 0 开始计数)执行异或运算得到。
请你找出 matrix 的所有坐标中第 k 大的值(k 的值从 1 开始计数)。
示例 1:
输入:matrix = [[5,2],[1,6]], k = 1
输出:7
解释:坐标 (0,1) 的值是 5 XOR 2 = 7 ,为最大的值。
示例 2:
输入:matrix = [[5,2],[1,6]], k = 2
输出:5
解释:坐标 (0,0) 的值是 5 = 5 ,为第 2 大的值。
示例 3:
输入:matrix = [[5,2],[1,6]], k = 3
输出:4
解释:坐标 (1,0) 的值是 5 XOR 1 = 4 ,为第 3 大的值。
示例 4:
输入:matrix = [[5,2],[1,6]], k = 4
输出:0
解释:坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ,为第 4 大的值。
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 1000
0 <= matrix[i][j] <= 10^6
1 <= k <= m * n
题目剖析&信息挖掘
此题主要考查动态规划,前缀和,排序算法的应用
解题思路
方法一 动态规划+前缀和+排序
分析
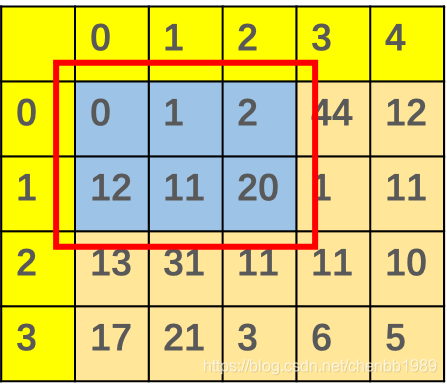
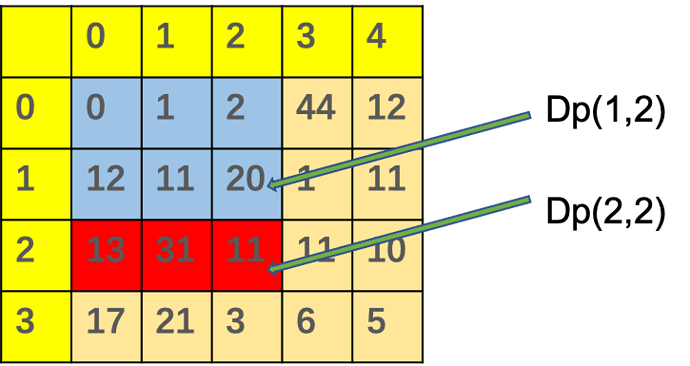
如图所示,在矩阵中红色框内所有数字异或值为矩阵中坐标 (1, 2) 的 值
设dp(a,b)矩阵中坐标 (a, b) 的 值。
从上图中可以看出 dp(2,2) = dp(1,2) ^ matrix[2][0]^ matrix[2][1]^ matrix[2][2]
那么我们得到动态规划的一个转移方程
dp(0,j) = matrix[0][0]^matrix[0][1]^...^matrix[0][j]
dp(i,j) = dp(i-1,j)^matrix[i][0]^matrix[i][1]^...^matrix[i][j]
matrix[0][0]^matrix[0][1]^...^matrix[0][j]的计算可以维护一个prexor[j]
prexor[j] = matrix[0][0]^matrix[0][1]^...^matrix[0][j] = matrix[i][j]^ prexor[j-1]
思路
func genDpArr(n, m int) [][]int{
dp := make([][]int , n)
for i:=0;i<n;i++ {
dp[i]=make([]int, m)
}
return dp
}
/*
dp(a,b) = 矩阵中坐标 (a, b) 的 值
dp(0,j) = matrix[0][0]^matrix[0][1]^...^matrix[0][j]
dp(i,j) = dp(i-1,j)^matrix[i][0]^matrix[i][1]^...^matrix[i][j]
*/
func kthLargestValue(matrix [][]int, k int) int {
n, m := len(matrix), len(matrix[0])
ans := make([]int, 0) // 存储所有可能的坐标值
prexor := make([]int, m) // 前缀和数组
dp := genDpArr(n, m)
for i:=0;i<n;i++ { // 遍历一行
// 计算前缀数组
// 计算矩阵中坐标 (i, j) 的 值
}
// 排序,这里是升序
sort.Ints(ans)
return ans[n*m-k] // 升序,所以要反着来
}
注意
- 注意边界,i,j =0时要特殊处理
- 代码里ans 是升序排序,所以是取ans[n*m - k]
知识点
- 动态规划
- 前缀和
- 排序
复杂度
- 时间复杂度:O(n*mlog(m*n))
- 空间复杂度:O(n*m)
代码实现
func genDpArr(n, m int) [][]int{
dp := make([][]int , n)
for i:=0;i<n;i++ {
dp[i]=make([]int, m)
}
return dp
}
/*
dp(a,b) = 矩阵中坐标 (a, b) 的 值
dp(0,j) = matrix[0][0]^matrix[0][1]^...^matrix[0][j]
dp(i,j) = dp(i-1,j)^matrix[i][0]^matrix[i][1]^...^matrix[i][j]
*/
func kthLargestValue(matrix [][]int, k int) int {
n, m := len(matrix), len(matrix[0])
ans := make([]int, 0)
prexor := make([]int, m)
dp := genDpArr(n, m)
for i:=0;i<n;i++ {
for j:=0;j<m;j++ {
// 计算前缀数组
prexor[j] = matrix[i][j]
if j>0 {prexor[j] = matrix[i][j]^prexor[j-1]}
// 计算矩阵中坐标 (i, j) 的 值
dp[i][j] = prexor[j]
if i>0 {
dp[i][j] = dp[i-1][j] ^ prexor[j]
}
ans = append(ans, dp[i][j])
}
}
sort.Ints(ans)
return ans[n*m-k]
}
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。