欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
题目描述
[1739] 放置盒子
题目描述
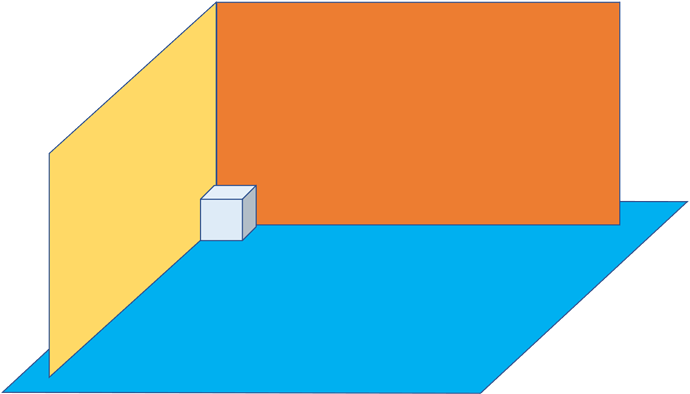
有一个立方体房间,其长度、宽度和高度都等于 n 个单位。请你在房间里放置 n 个盒子,每个盒子都是一个单位边长的立方体。放置规则如下:
你可以把盒子放在地板上的任何地方。
如果盒子 x 需要放置在盒子 y 的顶部,那么盒子 y 竖直的四个侧面都 必须 与另一个盒子或墙相邻。
给你一个整数 n ,返回接触地面的盒子的 最少 可能数量。
示例 1:
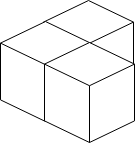
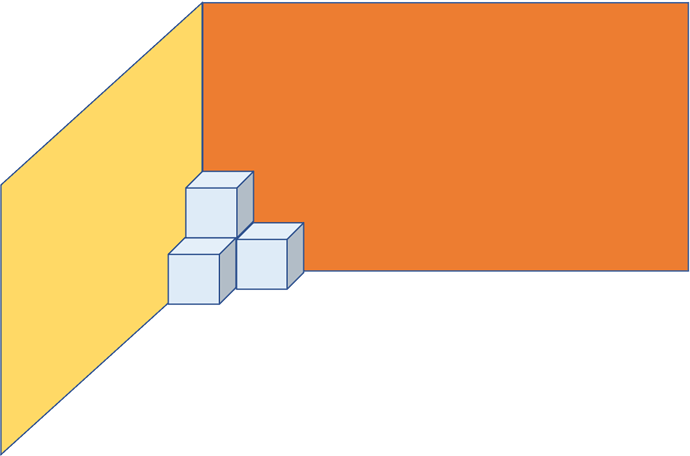
输入:n = 3
输出:3
解释:上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角,对应左侧位置。
示例 2:
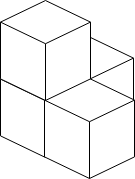
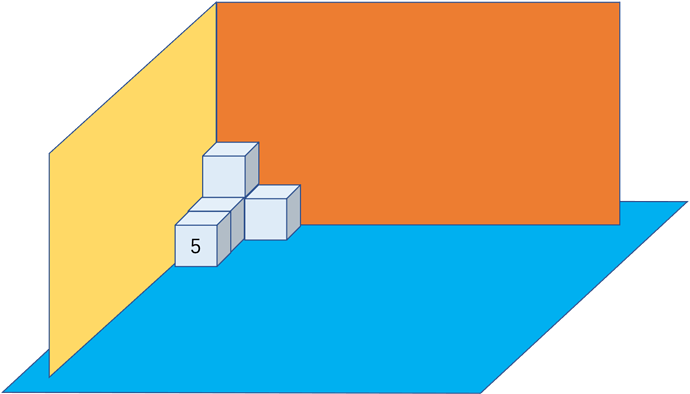
输入:n = 4
输出:3
解释:上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角,对应左侧位置。
示例 3:
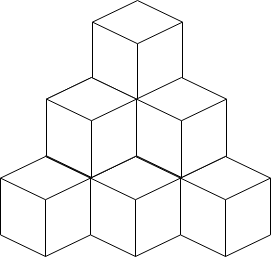
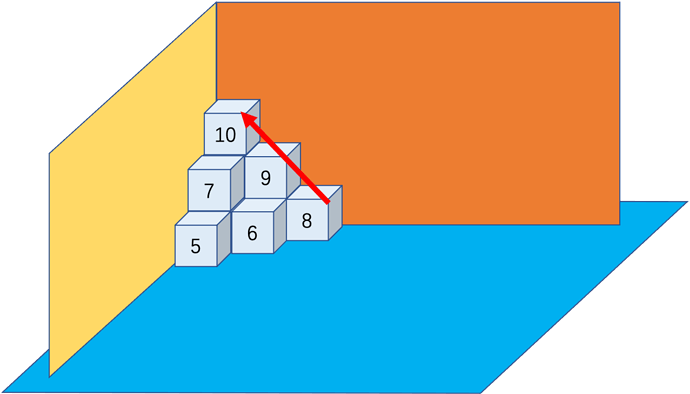
输入:n = 10
输出:6
解释:上图是 10 个盒子的摆放位置。
这些盒子放在房间的一角,对应后方位置。
提示:
1 <= n <= 10^9
题目剖析&信息挖掘
此题模板比较大,一般需要找到某种数学上的规律,然后通过模拟或动态规划解决。
解题思路
方法一 模拟+贪心+数学
分析
根据题意,先举几个特殊例子看看。
可以发现我们在放置盒子时,应该尽量与多的盒子贴近,以求上层可以放置更多的盒子。
从上面几个例子中可看出,在数量正好是1,4,10… 1+3+6+10+…+(1+n)*n/2时形状是完美的。
我们称像上面这样正好呈阶梯的形状为完美形状。
如果不是这些数量的话,可以从某一个特殊例子开始往上构造。
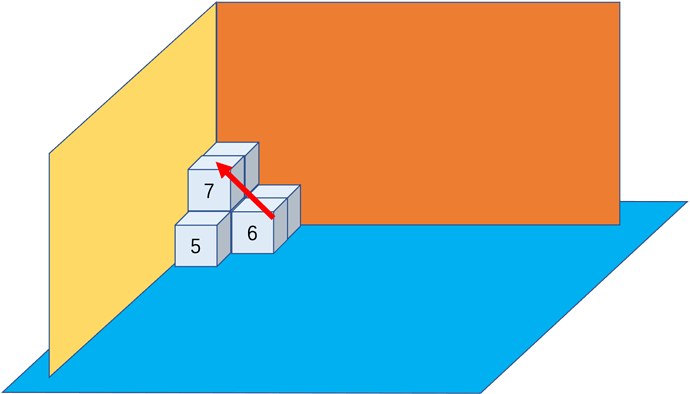
比如在这4个基础上再放置物体。
到这里我们可以发现一些规律。
在已经放置了2层(完美形状)情况下,每次都是从最底下开始,先往上放一个,再放2个,再3个。
推广到一般情况,如果当前已经放置了一个x-1层的完美形状。
那么接下来要放的就是斜向上放1个, 2个 ,3个 。。。x个。
下面我们看一下最底下个数与总数的关系。
| 底下个数 | n集合 | n的个数 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 3 | 3,4 | 2 |
| 4 | 5 | 1 |
| 5 | 6,7 | 2 |
| 6 | 8,9,10 | 3 |
| 7 | 11 | 1 |
| 8 | 12,13 | 2 |
| 9 | 14,15,16 | 3 |
| 10 | 17,18,19,20 | 4 |
| 11 | 21 | 1 |
| 12 | 22,23 | 2 |
| 13 | 24,25,26 | 3 |
| 14 | 27,28,29,30 | 4 |
| 15 | 31,32,33,34,35 | 5 |
| .。。 | 。。。 | 。。。 |
可看出规律,对于每一个底部数量,n的个数是呈等差数列变化的,从1到x1, 再从 从1到x2, 再从1到x3, 再从1到x4 … x = [1,2,3,4,…n]
总结一下就是每次往底部放一个,接下还可以放置y个(包括放在底部那个)使得底部数量不变化。这个y是遵从上述的多个等差数列分布的。
思路
func minimumBoxes(n int) int {
ans := 0
for step:=1;n>0;step++ { // 枚举当前层数,直到放到N个。
for i:=1;i<=step&&n>0;i++ { // 每次底部放置一个,接下来放置i个。直到放置n个。
n-=i // 接下来放置i个
ans++ // 底部旋转一个。
}
}
return ans;
}
注意
- n比较大,用减法不会溢出。
知识点
- 模拟
- 贪心
- 数学
复杂度
- 时间复杂度:O(sqrt(n))
- 空间复杂度:O(1)
代码实现
func minimumBoxes(n int) int {
ans := 0
for step:=1;n>0;step++ { // 枚举当前层数,直到放到N个。
for i:=1;i<=step&&n>0;i++ { // 每次底部放置一个,接下来放置i个。直到放置n个。
n-=i // 接下来放置i个
ans++ // 底部旋转一个。
}
}
return ans;
}
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。