AK F.*ing leetcode 流浪计划之二分查找

LightningBilly · 2021 年1 月 21 日 16:23

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

文章目录

[toc]

一、简介

二分查找算法是通过试探性的方法，逐步缩小答案范围，最终找到结果(最优解或无解)的一种搜索算法。

该算法每次可以排除当前解集中一半的不可行解。该算法要求解集具有单调性，即某一个解不可行时，那么大于或小于该解的解都不可行。

该算法的高效之处就在于每次可以排除一半的不可行解（或留下一半可能存在可行解），使得搜索次数大大减少，提高算法的效率。这也让我们在设计验证函数时可以适当的放开一些复杂度量极。

主要适用于数组中特定条件数字位置的查询，以及一些优值的求解应用。

二、条件及解题步骤

条件：

解集是一个数字区间[l, 4], 必须有 1）有序性，2）线性的（随着数字的增大或减小离最优解越近或越远）3）可以随机访问。
对于某一个解，可以比较方便(复杂度不高)去判断该解是否可行。即可以设计出效率不低的验证方法checkFunc。

解题步骤

判断是否可以用二分

确定解集范围 [l, r]，并且是否满足有序且线性。
设计验证可行解函数 checkFunc。

具体操作

step 1 初始化 [l, r]，best

step 2 计算出中间值 mid

step 3 checkFunc(mid)

step 4 根据check 结果记录最优值best，并重新确定[l, r] (或者确定找到最优解返回结束)

step 5 如果l<=r 则跳转到step 2.

三、作用

常规数组查询

查询数组中特定的数字
查询数字存在的上下界
查询大于或小于某数字的上下界
翻转有序数组中一些问题的应用

推广到一般问题求最优解应用

求解平方根。
求解软件最近可用版本。
在一些求解最大或最小值问题中，不能通过动态规划，贪心等方法直接求出，但是可以验证某个值的可行性时，可以考虑二分。

四、代码框架

在有序数组查询中，固定值查询（是否存在），上下界查询是比较常用的操作。也被写成了模板，我在初学理解时，被三个模板的差异搞得很迷糊。其中主要的变化是1）终止条件的判断（l<r or l<=r or l+1<r）什么时候用哪个；2）mid 的确定，mid = (left+right)/2 (向下取整 or 向上取整)。理解各中原理固然重要，但如果每次做新题目时，都要去考虑这些问题，那么无疑对做题效率以及准确性方面会大打折扣。下面我先给出经典问题的标准写法以及其中原理，再抛出我总结的一般模板。

经典算法

在有序数组中查找定值

func BinarySearch(a []int, value int) int {
	low, high := 0, len(a)-1

	for low <= high {
		mid := (low + high) >> 1
		if a[mid] == value { // 找到答案直接返回
			return mid
		}
		
		if a[mid] < value { // mid 以及 < mid 都不可能是答案
			low = mid + 1
		} else { // mid 以及 > mid 都不可能是答案
			high = mid - 1
		}
	}
	return -1
}

在有序数组中查找定值最左位置

func findFirstPosition(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left < right {
		mid := (right + left) / 2
		// 小于一定不是解
		if nums[mid] < target {
			// 下一轮搜索区间是 [mid + 1, right]
			left = mid + 1
		} else if nums[mid] == target {
			// 下一轮搜索区间是 [left, mid]
			right = mid
		} else {
			// nums[mid] > target，下一轮搜索区间是 [left, mid - 1]
			right = mid - 1
		}
	}

	// 此处要特判
	if nums[left] == target {
		return left
	}
	return -1
}

在有序数组中查找定值最右位置

func findLastPosition(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left < right {
		mid := left + (right - left + 1) / 2 // 默认往高位走
		if nums[mid] > target {
			// 下一轮搜索区间是 [left, mid - 1]
			right = mid - 1
		} else if nums[mid] == target {
			// 下一轮搜索区间是 [mid, right]
			left = mid
		} else {
			// nums[mid] < target，下一轮搜索区间是 [mid + 1, right]
			left = mid + 1
		}
	}
	return left
}

从上面三个算法中看出，每个算法的终止条件，right, left 重新取值，还有外面的特判都有所差别。相信写过二分算法的人都知道，经常产生数组越界，边界考虑不周等情况，最后针对用例编程，搞得代码面目全非。如果每来个新题目都要关注这些点，非常容易出错，编码效率也大大降低。

二分模板

从上面几个模板可以看出，我们要求的其实是一个最优解。由于解集本身具有单调性，那么全局最优解必然也是局部最优解。我们可以在第一个算法基础上，开一个变量best来保存当前的最优解，每次遇到可行解时都去更新最优解，算法终止时best必然也是全局最优解。

func BinarySearch(a []int, value int) int {
	low, high := 0, len(a)-1
  	best := -1 // 默认无解，也可以根据需要置其他特殊值
	for low <= high {
		// mid := (low + high) >> 1
	    // 有时候low, high比较大，求和会溢出
	    mid := low + (high-low)/2
	    
	    // 以下根据检查结果，更新best, left, right
	    switch checkFunc(mid) {
	      case 1:
	      	...
	      case 2:
	      	...
	      	...
	    }
	}
	return best
}

以上模板中终止条件和mid的生成是固定，我们要关心的是里面具体的逻辑。根据检查结果不同，再加上贪心原则，去更新best, low, high。

重写在有序数组中查找定值最左位置

func checkFunc(midVal, target int) int {
	if midVal == target {
		return 0
	}
	if midVal< target {
		return -1
	}

	return 1
}

func findFirstPositionV2(nums []int, target int) int {
	left, right := 0, len(nums)-1
	best := -1
	for left <= right {
		mid := (right + left) / 2
		checkRes := checkFunc(nums[mid], target)

		if checkRes == 0 { // 目前是一个可行解，保存该解为当前最优解，并把范围向右缩小查看是否还有更小
			best, right = mid, mid-1 // mid已经检测了，检查右边即可
		} else if checkRes<0 { // 当前位置比目标小，需要往右移使数字增大
			left = mid+1
		} else { // 当前位置比目标大，需要往左移使数字减小
			right = mid-1
		}
	}

	return best
}

在上面代码中，如果没有答案，那么checkFunc结果永远不为0，即best无解。

终止条件 left <= right ，以及更新left, right的方式保证每个数字都可能被检测到并且不需要考虑越界的情况。

每次找到更优答案后会贪心去查看更左边有没有答案。

最终可以得到最左边与目标相等的位置。

五、牛刀小试

练习1 x 的平方根

题目链接力扣

题目大意

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2
示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。

题目解析

根据题意，是查找一个最大整数a使得a^2<=x。

显然范围可以设置为 [0, x]，具有线性性，可以随机访问。

检测函数就是mid^2<=x。

更新best, left, right逻辑

如果 mid^2<=x 则best, left = mid, mid+1.

否则right = mid-1

注意，1)由于x = [0, intmax32]。mid := left + (right-left)/2

mid*mid 有可能超出 int范围，可以用mid<=x/mid代替mid^2<=x, (mid >0, 0的情况一开始就判断)

AC代码

func mySqrt(x int) int {
	if x==0 {return 0}
	left , right := 1, x
	best := -1

	for left <= right {
		mid := left + (right-left)/2
		if mid <= x/mid { // 可行解，更新最优解，并查看有没有更优
			best, left = mid, mid+1
		} else {// 不可行解，查看更小解
			right = mid-1
		}
	}

	return best
}

练习2 供暖器

题目链接：力扣

题目大意

冬季已经来临。你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。

在加热器的加热半径范围内的每个房屋都可以获得供暖。

现在，给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置，请你找出并返回可以覆盖所有房屋的最小加热半径。

说明：所有供暖器都遵循你的半径标准，加热的半径也一样。

示例 1:

输入: houses = [1,2,3], heaters = [2]
输出: 1
解释: 仅在位置2上有一个供暖器。如果我们将加热半径设为1，那么所有房屋就都能得到供暖。
示例 2:

输入: houses = [1,2,3,4], heaters = [1,4]
输出: 1
解释: 在位置1, 4上有两个供暖器。我们需要将加热半径设为1，这样所有房屋就都能得到供暖。
示例 3：

输入：houses = [1,5], heaters = [2]
输出：3

提示：

1 <= houses.length, heaters.length <= 3 * 10^4
1 <= houses[i], heaters[i] <= 10^9

题目解析

可以知道加热半径范围是[0，10^9], 具有线性性，可以随机访问。

可以尝试给定一个半径，测试以这个半径是不是可以供暖全部房屋。

checkFunc 设计如下

先对房屋和暖气进行排序。

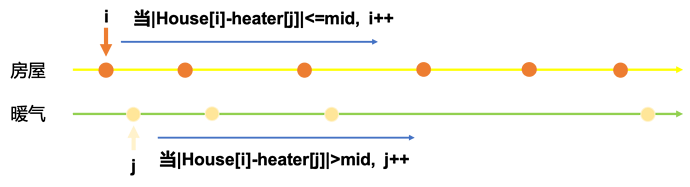
由于所有的房屋都要供应到。贪心原理，初始i, j=0,0。检查当前暖气是否可以照到当前房屋。如果不行，说明要么当前暖气太在左边了，需要看看右边的暖气可不可以照到。要么是暖气太在右边了（再往后移也不行了）。

最后，判断一下i==len(House)。

利用双指针法, 复杂度O(n+m)

总复杂度 O(log(10^9) * (m+n))

思路

func checkFunc(houses []int, heaters []int, radius int) bool {

}


func findRadius(houses []int, heaters []int) int {
	// 排序
	sort.Slice(houses, func(i, j int) bool {
		return houses[i]<houses[j]
	})
	sort.Slice(heaters, func(i, j int) bool {
		return heaters[i]<heaters[j]
	})
	best := int(10e9)
	left, right := 0, int(10e9)
	for left<= right {
		mid := (right+left)>>1
		if checkFunc(houses, heaters, mid) { // 可行解，贪心查看有没有更好解, 区间往小移
			best, right = mid, mid-1
		} else {
			left = mid+1
		}
	}

	return best
}

AC代码

func abs(a int) int {
	if a<0 {return -a}
	return a
}
func checkFunc(houses []int, heaters []int, radius int) bool {
	i, j:=0,0
	for ;i<len(houses) && j<len(heaters); {
		if abs(houses[i] - heaters[j])<=radius{
			i++
		}else {j++}
	}
	return i==len(houses)
}

func findRadius(houses []int, heaters []int) int {
	// 排序
	sort.Slice(houses, func(i, j int) bool {
		return houses[i]<houses[j]
	})
	sort.Slice(heaters, func(i, j int) bool {
		return heaters[i]<heaters[j]
	})
	best := int(10e9)
	left, right := 0, int(10e9)
	for left<= right {
		mid := (right+left)>>1
		if checkFunc(houses, heaters, mid) { // 可行解，贪心查看有没有更好解, 区间往小移
			best, right = mid, mid-1
		} else {
			left = mid+1
		}
	}

	return best
}

/*
[1,2,3]
[2]
[2]
[2]
[1,2,3,4]
[1,4]
[1,5]
[2]
[4,3,2,1]
[1,4]
*/

六、代码模板

func BinarySearch(a []int, value int) int {
	low, high := 0, len(a)-1
  best := -1 // 默认无解，也可以根据需要置其他特殊值
	for low <= high {
		// mid := (low + high) >> 1
    // 有时候low, high比较大，求和会溢出
    mid := low + (high-low)/2
    
    // 以下根据检查结果，更新best, left, right
    switch checkFunc(mid) {
      case 1:
      	...
      case 2:
      	...
      	...
    }
	}
	return best
}

此模板适用于只需要一个验证可行解的函数，有些情况下判断可行解可能有多层嵌套判断，需要适当改造，不过此模板已经适用于大多数情况。

七、总结

主要内容：

二分查找算法是通过试探性的方法，逐步缩小答案范围，最终找到结果(最优解或无解)的一种搜索算法。
适用条件
- 解集是一个数字区间[l, 4], 必须有 1）有序性，2）线性的（随着数字的增大或减小离最优解越近或越远）3）可以随机访问。
- 对于某一个解，设计出验证函数checkFunc去验证可行性。
解题的基本框架比较固定，关键在于checkFunc的设计，以及解区间的确定。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），有些leetcode题目不是很容易看出来二分思路，可略过。给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

八、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动用把刚才那2题A了。

x 的平方根题目链接力扣
供暖器题目链接力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

力扣二分查找题目列表

以上题目太多，大家适当选择就行，下面还有进阶题目。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

poj

http://poj.org/problem?id=3349

以下将序号替换就是题目链接。

3349
3274
1840
2002
2503
3122
1064
3579
2503
3977

hdu

http://acm.hdu.edu.cn/showproblem.php?pid=1597

以下将序号替换就是题目链接。

1597 find the nth digit
2578
2141
3763
2199
2899
1969
4768

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。

在这里插入图片描述

kingeasternsun · 2021 年2 月 7 日 02:04

二分加贪心求最长递增子序列