欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
@[toc]
题目描述
[1727] 重新排列后的最大子矩阵
给你一个二进制矩阵 matrix ,它的大小为 m x n ,你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后,全是 1 的子矩阵面积。
示例 1:
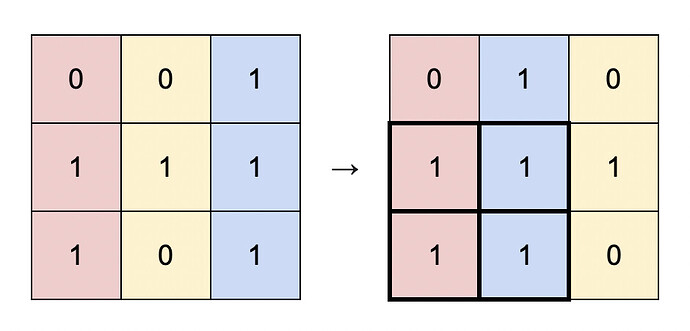
输入:matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 4 。
示例 2:
输入:matrix = [[1,0,1,0,1]]
输出:3
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 3 。
示例 3:
输入:matrix = [[1,1,0],[1,0,1]]
输出:2
解释:由于你只能整列整列重新排布,所以没有比面积为 2 更大的全 1 子矩形。
示例 4:
输入:matrix = [[0,0],[0,0]]
输出:0
解释:由于矩阵中没有 1 ,没有任何全 1 的子矩阵,所以面积为 0 。
提示:
m == matrix.length
n == matrix[i].length
1 <= m * n <= 10^5
matrix[i][j] 要么是 0 ,要么是 1 。
题目剖析&信息挖掘
此题主要用枚举思想,将复杂问题简化,再利用贪心思想求解。
解题思路
方法一 枚举+贪心
分析
题目说每一列可以动,但是行不可以动。由于题目说是要取其中的一个子矩阵,矩阵的上下边界必然是某一行。
我们可以尝试枚举某一行row[i]为矩阵的底,求解出row[i]为底的最解best[i]。
答案就是max(best[x]) x = [0, len(matrix)-1]。
来看一下row[i]为底时,要面对的问题。
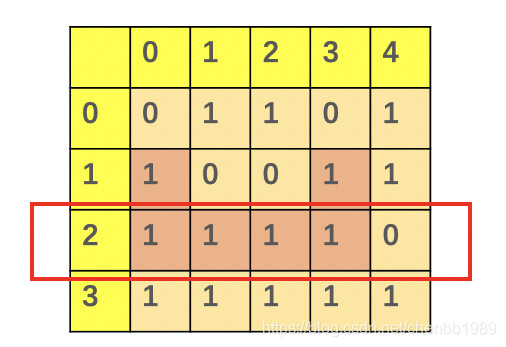
在上图中,以row[2]为底,那么红色中的1才是有效的区域,其他列不管怎么移,也不能满足以row[2]为底构造出一个矩阵。
那么现在的问题就转化为在同一平面上给出一些宽度为1,高度不等的长方形,问如何移动得到一个最大的矩形。
设数组h,长度为len(row[i]), h[j]表示从row[i][j]开始向上连续为1的个数。
上图中h = [2,1,1,2,0]。枚举高度为x = [1, max(h[i])], 查看高度>=x 的数量 c, 取所有x*c 最大值即为答案。查找数量c可以对h进行排序解决。
思路
- 初始h = [0,0,…,0]
- 对于一行row[i], 如果row[i\][j]=0, 则h[j]=0,否则h[j]++。
- 计算出当前行为底的最优解。
- 求出所有行为底的最优解,综合取最大值。
- 复杂度:遍历一行并求解复杂度为O(mlog(m)), 总体O(n*mlog(m))
func largestSubmatrix(matrix [][]int) int {
lenArr := make([]int, len(matrix[0])) // 存储当前高度
best :=0 // 存储最优解
for _, row := range matrix {
// 遍历当前行并计算高度
// 计算当前行为底的最优解
}
return best
}
func max(a, b int) int {
if a>b{return a}
return b
}
注意
- 求解时原来的h数组不能换顺序,要自己重新复制一份。
知识点
- 枚举
- 贪心
复杂度
- 时间复杂度:O(n*mlog(m))
- 空间复杂度:O(n*m)
代码实现
func largestSubmatrix(matrix [][]int) int {
lenArr := make([]int, len(matrix[0])) // 存储当前高度
best :=0 // 存储最优解
for _, row := range matrix {
// 遍历当前行并计算高度
for i, v := range row {
if v ==0 {
lenArr[i]=0
} else {lenArr[i]++}
}
// 计算当前行为底的最优解
tempArr := make([]int, len(lenArr)) // 复制备份,不要破坏原来的数组
copy(tempArr,lenArr)
sort.Slice(tempArr, func(a, b int ) bool {return tempArr[a]>tempArr[b]})
for i, v := range tempArr {
best = max(best, (i+1)*v)
}
}
return best
}
func max(a, b int) int {
if a>b{return a}
return b
}
相关题目
https://leetcode-cn.com/problems/maximal-rectangle/
https://leetcode-cn.com/problems/maximal-square/
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/