AK F.*ing leetcode 流浪计划之并查集

算法之美
,
1

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

文章目录

一、简介
二、定义
三、作用
四、数据定义及算法
数据定义
算法描述
五、具体实现
六、牛刀小试
练习1 判连通应用
题目大意
题目解析
AC代码
练习2 求解连通块应用
题目大意
题目解析
思路
AC代码
七、问题及优化
压缩路径
平衡合并
八、代码模板
九、总结
十、实战训练
代码基础训练题
AK leetcode
大神进阶

一、简介

并查集数据结构在平时的算法中非常常用，操作比较简单，代码少，好理解，好实现，学习成本低。
同时，也是很多复杂算法里的一个辅助算法。

二、定义

并查集是一种树（森林）型的数据结构。
将编号分别为1-N的N个对象划分为不相交集合。
在每个集合（树）中，选择其中1个元素（树的根）代表所在集合。
能够高效的实现对集合进行合并和查询集合中元素的关系。

三、作用

  1. 最常用的就是在图中判断2个点是否连通。
  2. 求解连通块数量
  3. 类似一些问题也是转化为图模型去使用并查集模板。
  4. 也有针对实际场景，添加（修改）并查集属性，来实现其他附属信息的查询。

四、数据定义及算法

并查集是一种树型结构，数据结构中可以用邻接表法，矩阵法，和父结点法来表示树，这里利用最简单的父结点表示法。

数据定义

UnoinFindSet {
    father array // 数组 father[i]表示i结点的父亲，如果father[i]=i, 由表示i为自己所在集合的代表。
    // 操作有3种：
    InitSet(n): // 初始化数据
    Find(x)：// 查找x所在集合的代表
    Union(x, y) // 将x, y所在集合合并
}

算法描述

请添加图片描述
请添加图片描述619×519 107 KB

请添加图片描述
请添加图片描述951×729 63.5 KB

请添加图片描述
请添加图片描述1194×850 90.4 KB 

InitSet(n): // 初始化数据
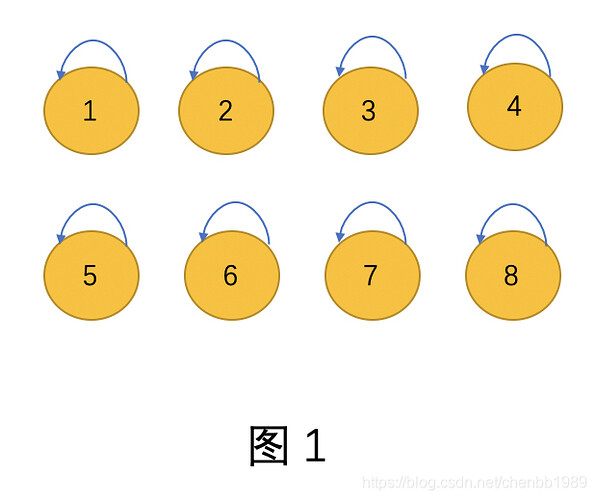
    // 遍历所有结点并初始化所有点的父亲都是自己 如图1
    for i <- 1 to n do
        father[i]<-i

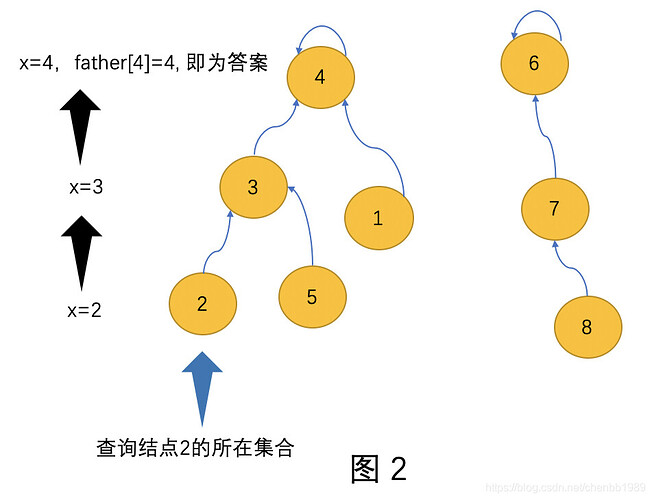
Find(x)：// 查找x所在集合的代表
    // 一直查找自己的父亲，直到father[x]=x, 返回x 图2
    while father[x]!=x do
        x <- father[x]
    end
    return x

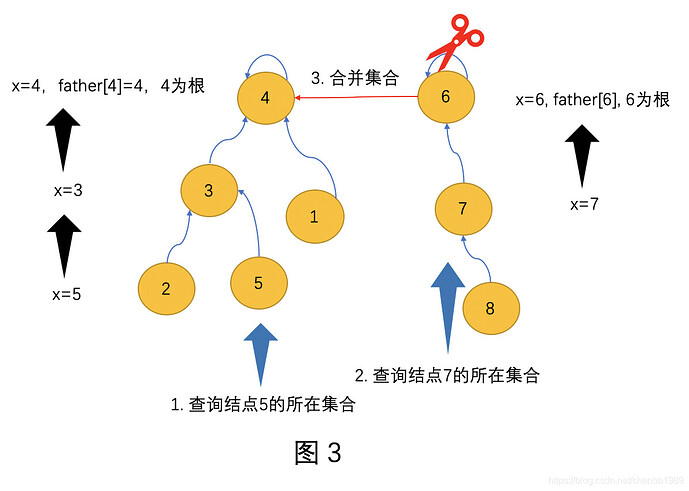
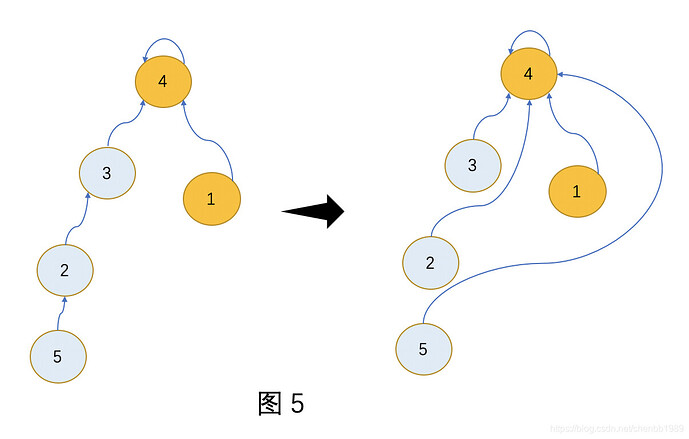
Union(x, y): // 将x, y所在集合合并
    // 注意这里是合并x, y所在「集合」，不是合并x,y
    // 先找到x, y的集合代表，使其代表的父亲=另一个，如图3
    x<-Find(x)
    y<-Find(y)
    // 由于并查集是一个树型，树型是有向无环图。
    // 无环意味着已经连通的点不能再加边，所以x==y时，忽略。
    if x!=y do 
        father[x] = y

五、具体实现

这里先用go实现一下，后续我会把C++版本整合到github上，地址：GitHub - LightningBilly/ACMAlgorithms


package main
import "fmt"

/*
并查集，判连通用
*/
type UnionFindSet struct {
   father  []int // 存储结点的父亲
   nodeNum int   // 总结点个数
}

func (us *UnionFindSet) InitUnionSet(n int) {
   us.nodeNum = n+1 // 不加也可以，有人喜欢以0开头
   us.father = make([]int, us.nodeNum)
   for i, _ := range us.father {
      us.father[i] = i
   }
}

// 查询父结点
func (us *UnionFindSet) Find(x int) int {
   for us.father[x] != x {
      x = us.father[x]
   }
   return x
}

//合并结点
func (us *UnionFindSet) Union(x, y int) bool {
   x = us.Find(x)
   y = us.Find(y)
   if x == y {
      return false
   }
   us.father[x] = y
   return true
}

func main() {
   us:= &UnionFindSet{}
   us.InitUnionSet(11)
   us.Union(1, 2)
   us.Union(10, 9)
   us.Union(7,8)
   us.Union(8,3)
   us.Union(8,9)

   for i:=0;i<=10; i++  {
      fmt.Println(i, us.Find(i))
   }
}

六、牛刀小试

练习1 判连通应用

题目链接 http://hihocoder.com/problemset/problem/1066, 无间道之并查集 - HihoCoder 1066 - Virtual Judge

题目大意

有2种操作，
0表示将2人划为同一阵营
1表示查询2人是否为同一阵营

注：同一阵营关系具有传递性：a与b同一阵，b与c同一阵营，那么a与c也是同一阵营。
要求遇到查询操作时，输出2人是否为同一阵营

输入：
第一行一个N表示以下会有N个操作
接下来n行，每行3个元素，一个数字，2个字符串，o a b。
o代表操作取值0，1如上所述。a b代表人员名字。
满足N<=10^5, 且数据中所有涉及的人物中不存在两个名字相同的人（即姓名唯一的确定了一个人），对于所有的操作，a和b是不同的两个人。

输出：
如果遇到查询操作（o=1)则输出a b是否为同一阵营，是则输出yes，否则输出no。

数据规模：
N<=10^5

题目解析

0操作就是Union操作
1操作就是判断2人是不是在同一集合，只要找到集合代表比较就可以了。
题目输入的不是数字，需要把名字编号。
由于每个人名不同，只要根据名字给定不同数字就可以了。我这里利用数字递增法生成，即每来一个新名字，编号+1.

AC代码


#include <iostream>
#include<vector>
#include<string>
#include<cstring>
#include<stdio.h>
#include <queue>
#include<map>
#include <algorithm>

using namespace std;


class UnionFindSet {
private:
    vector<int> father; // 父结点定义，father[i]=i时，i为本集合的代表
    int nodeNum; // 集合中的点数

public:
    UnionFindSet(int n); // 初始化
    bool Union(int x, int y); // 合并
    int Find(int x);
};

UnionFindSet::UnionFindSet(int n) : nodeNum(n + 1) {
    father = vector<int>(nodeNum);
    for (int i = 0; i < nodeNum; ++i) father[i] = i; // 初始为自己
}

int UnionFindSet::Find(int x) {
    while (father[x] != x) x = father[x];
    return x;
}

bool UnionFindSet::Union(int x, int y) {
    x = Find(x);
    y = Find(y);

    if (x == y)return false;
    father[x] = y;
    return true;
}

/*
编号生成器
原理：查看名字是否编号，有则直接返回，没有则将其编号为目前最大的数字。
*/
class IndexMaker {
private:
    int curUsedIndex;
    map<string, int> indMap;
public:
    IndexMaker();
    int GetIndByName(string name);
};

// 初始化当前编号为0
IndexMaker::IndexMaker() : curUsedIndex(0) {
    indMap.clear();
}

int IndexMaker::GetIndByName(string name) {
  	// 如果没有编号，则添加编号
    if (indMap.count(name) == 0) indMap[name] = curUsedIndex++;
    return indMap[name];
}

int main() {

    int n;
    cin >> n;
    UnionFindSet us(2 * n); // 最多有可能2n个人

    string a, b;
    int o;
    IndexMaker indMaker;

    for (int i = 0; i < n; ++i) {
        cin >> o >> a >> b;
        int indexa = indMaker.GetIndByName(a), indexb = indMaker.GetIndByName(b);
        if (o == 0) us.Union(indexa, indexb);
        else {
            int roota = us.Find(indexa), rootb = us.Find(indexb);
            string ans = roota == rootb ? "yes" : "no";
            cout << ans << endl;
        }
    }
}


/**

10
0 Steven David
0 Lcch Dzx
1 Lcch Dzx
1 David Dzx
0 Lcch David
0 Frank Dzx
1 Steven Dzx
1 Frank David
0 Steven Dzx
0 Dzx Frank
样例输出
yes
no
yes
yes

*/

练习2 求解连通块应用

题目链接：力扣

题目大意

班上有 N 名学生。其中有些人是朋友。朋友关系是可以传递的。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示学生之间的朋友关系。如果M[i][j] = 1，表示第 i 个和 j 个学生互为朋友关系。输出朋友圈总数。

题目解析

一个朋友圈内的同学是互为朋友关系，就是在同一个集合里。
那么我们只要对所有朋友关系的同学进行合并，然后查看有多少个不同的集合即可。
一个集的代表只有一个，只要能找出这个代表（标志就是Find(x)=x）就可以统计出不同集合的个数。

思路

func findCircleNum(M [][]int) int {
	us.InitUnionFindSet(n)
	for i<-1-n {
    for j<- 1-n {
      if i和j是朋友 : us.Union(i,j)
    }
	}
	
	friendCircle <- 0
	for i<-1-n {
    if us.Find(i)==i : friendCircle <- friendCircle+1
	}
	
	return friendCircle
}

AC代码


/*
并查集，判连通用
*/
type UnionFindSet struct {
	father  []int // 存储结点的父亲
	nodeNum int   // 总结点个数
}

func (us *UnionFindSet) InitUnionSet(n int) {
	us.nodeNum = n+1
	us.father = make([]int, us.nodeNum)
	for i, _ := range us.father {
		us.father[i] = i
	}
}

// 查询父结点
func (us *UnionFindSet) Find(x int) int {
	for us.father[x] != x {
		x = us.father[x]
	}
	return x
}

//合并结点
func (us *UnionFindSet) Union(x, y int) bool {
	x = us.Find(x)
	y = us.Find(y)
	if x == y {
		return false
	}
	us.father[x] = y
	return true
}

func findCircleNum(M [][]int) int {
	us := &UnionFindSet{}
	us.InitUnionSet(len(M))
	for i,row:=range M{
		for j,isFriend :=range row {
		if isFriend==1 {us.Union(i,j)} // 是朋友则合并
	}
	}

	friendCircle :=0 
	for i:=0;i<len(M);i++ {
		if us.Find(i)==i { friendCircle++} // 查看集合代表个数
	}

	return friendCircle
}
/*
[[1,1,0],[1,1,0],[0,0,1]]
[[1]]
[[1,0,0],[0,1,0],[0,0,1]]
[[1,0,1],[0,1,0],[1,0,1]]
[[1,0,1,0],[0,1,0,0],[1,0,1,1],[0,0,1,1]]
*/

七、问题及优化

压缩路径

Find(x)：// 查找x所在集合的代表
    // 一直查找自己的父亲，直到father[x]=x, 返回x 图2
    while father[x]!=x do
        x <- father[x]
    end
    return x

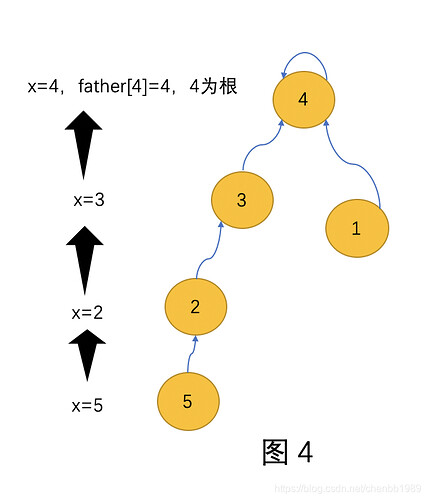
在这里插入图片描述
在这里插入图片描述680×797 93.9 KB

看Find操作，可以发现最坏情况下，操作的复杂度是O(n)。

通过观察可以发现在查找结点5的根时，其实结点2，3只是起到一个中间桥梁的作用，最后实际返回的是4。

其实我们最后想得到的是 find(5)=find(2)=find(3)=find(4)=4。

那么我们就可以对树进行以下操作。

在这里插入图片描述
在这里插入图片描述1206×768 67.5 KB

把结点5到根的路径上所有的结点直接指向4，这个操作叫做"路径压缩"。

这样做的好处在于，这次查询是O(n)的，将来其他的2，3结点查询是o(1), 均摊下来的话，就是O(1)。

优化后的代码查询代码：

// 查询父结点
func (us *UnionFindSet) Find(x int) int {
	 root := x // 保存好路径上的头结点
   for us.father[root] != root {
      root = us.father[root]
   }
   /*
   从头结点开始一直往根上遍历
   把所有结点的father直接指向root。
   */
   for us.father[x] != x {
   		// 一定要先保存好下一个结点，下一步是要对us.father[x]进行赋值
   		temp := us.father[x] 
      us.father[x] = root
      x = temp
   }
   
   return root
}
这一步优化已经满足绝大多数场景，下面的平衡合并可以了解一下。

平衡合并

看这么一个例子，图6

在这里插入图片描述
在这里插入图片描述981×603 60.2 KB

可以看到极端情况下会退化成一个链表。对于查询效率也是有影响的。

还记得二叉查找树么，也有类似的情况。他的解决办法是让树平衡(左右子树高度差不大于1)。

对于并查集的解决办法是尽量让左右子树平衡(高度相差尽量小点)。

规则如下：

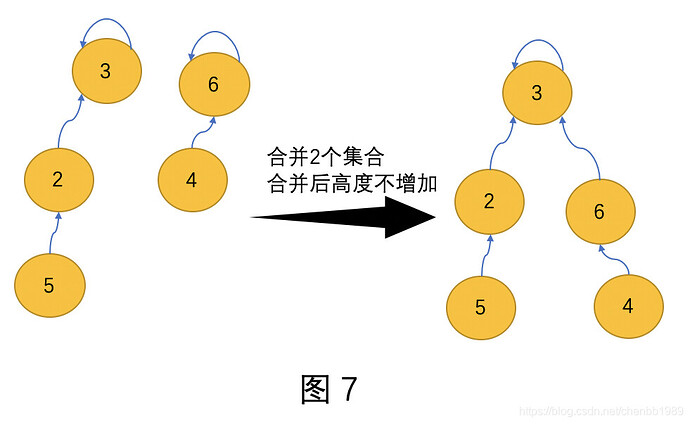
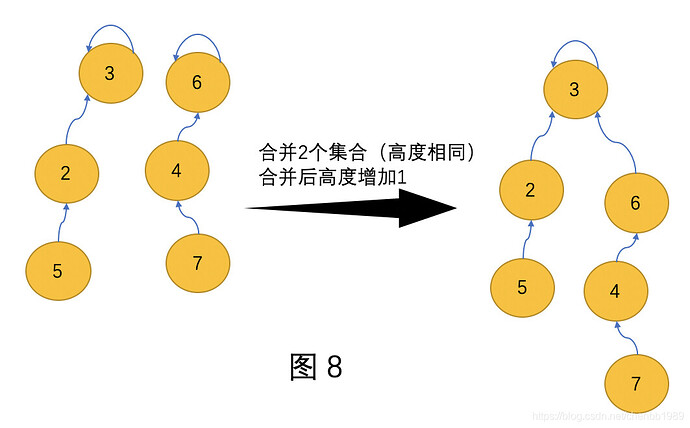
假设现在集合a(root是a), 集合b(root是b) 要合并。

集合a的高度是ha, 集合b的高度是hb。分3种情况讨论。

1）ha < hb: father[a]=b(让b成为集合a的根), hb不变，如图7

2）ha > hb: father[b]=a(让a成为集合b的根), ha不变，与上同理

  1. ha == hb: 需要判断 a==b ? 如果是就不操作(原来就在一个集合里，不需要操作)，否则father[a]=b, hb++(反之亦可。)如图8，注意树的高度要加1

在这里插入图片描述
在这里插入图片描述1063×660 71.2 KB

在这里插入图片描述
在这里插入图片描述981×603 60.2 KB 

/*
需要加入height[]属性，初始化为1.
*/
//合并结点
func (us *UnionFindSet) Union(x, y int) bool {
   x = us.Find(x)
   y = us.Find(y)
   if x == y {
      return false
   }
   if us.height[x]<us.height[y] {
     us.father[x]=y
   } else if us.height[x]>us.height[y] {
     us.father[y]=x
   } else {
     us.father[x] = y
     us.height[y]++
   }
   return true
}

八、代码模板

package main
import "fmt"

/*
并查集，判连通用
*/
type UnionFindSet struct {
	father  []int // 存储结点的父亲
	height  []int // 存储树的高度
	nodeNum int   // 总结点个数
}

func (us *UnionFindSet) InitUnionSet(n int) {
	us.nodeNum = n+1 // 不加也可以，有人喜欢以0开头
	us.father = make([]int, us.nodeNum)
	us.height = make([]int, us.nodeNum)
	for i, _ := range us.father {
		us.father[i] = i
		us.height[i] = 1
	}
}

// 查询父结点
func (us *UnionFindSet) Find(x int) int {
	for us.father[x] != x {
		x = us.father[x]
	}
	return x
}

//合并结点
func (us *UnionFindSet) Union(x, y int) bool {
	x = us.Find(x)
	y = us.Find(y)
	if x == y {
		return false
	}
	us.father[x] = y
	return true
}

func (us *UnionFindSet) FindV2(x int) int {
	root := x // 保存好路径上的头结点
	for us.father[root] != root {
		root = us.father[root]
	}
	/*
	从头结点开始一直往根上遍历
	把所有结点的father直接指向root。
	*/
	for us.father[x] != x {
		// 一定要先保存好下一个结点，下一步是要对us.father[x]进行赋值
		temp := us.father[x]
		us.father[x] = root
		x = temp
	}

	return root
}

/*
需要加入height[]属性，初始化为1.
*/
//合并结点
func (us *UnionFindSet) UnionV2(x, y int) bool {
	x = us.Find(x)
	y = us.Find(y)
	if x == y {
		return false
	}
	if us.height[x]<us.height[y] {
		us.father[x]=y
	} else if us.height[x]>us.height[y] {
		us.father[y]=x
	} else {
		us.father[x] = y
		us.height[y]++
	}
	return true
}

func main() {
	us:= &UnionFindSet{}
	us.InitUnionSet(11)
	us.UnionV2(1, 2)
	us.UnionV2(10, 9)
	us.UnionV2(7,8)
	us.UnionV2(8,3)
	us.UnionV2(9,8)

	for i:=0;i<=10; i++  {
		fmt.Println(i, us.FindV2(i))
	}
}

九、总结

主要内容：

  1. 并查集是一种树型结构，能够高效实现的对集合进行合并和查询集合中元素的关系。
  2. 作用：1）判断2个点是否连通；2）求解连通块数量；3）也有更深入的用法，要自己探索。
  3. 可以通过路径压缩和平衡合并来优化查询效率。

初学一个算法时最好在纸上把所有过程自己模拟一遍，理清思路，要对过程了然于心。当然，这也不是一蹴而就的，要在做题中不断应用。每次应用就相当于在心里过了一遍历。慢慢的就感觉对这个过程很了解，就算很久没用，偶尔让写一下还是可以写出来。

笔者水平有限，有写得不对或者解释不清楚的地方还望大家指出，我会尽自己最大努力去完善。

下面我精心准备了几个流行网站上的题目（首先AK F.*ing leetcode），给大家准备了一些题目，供大家练习参考。干他F.*ing (Fighting?)。

十、实战训练

代码基础训练题

光说不练假把式，学完了怎么也要实操一下吧，快快动用把刚才那2题A了。

  1. 连通性应用 http://hihocoder.com/problemset/problem/1066, 无间道之并查集 - HihoCoder 1066 - Virtual Judge
  2. 连通块个数应用 力扣

AK leetcode

leetcode相关题目都在下面了，拿起武器挨个点名呗。

力扣 并查集题目列表

做完以上还觉得不过瘾，我给大家还准备了一些。

大神进阶

也可以去vjudge Problems - Virtual Judge 搜索相关题号

poj

http://poj.org/problem?id=1988

以下将序号替换就是题目链接。

  1. 1182
  2. 1308
  3. 1417
  4. 1456
  5. 1611
  6. 1733
  7. 1861
  8. 1984
  9. 1986
  10. 1988
  11. 2236
  12. 2492
  13. 2524
  14. 2912
  15. 3038

hdu

http://acm.hdu.edu.cn/showproblem.php?pid=1198

以下将序号替换就是题目链接。

  1. 1198
  2. 1213
  3. 1232
  4. 1272
  5. 1299
  6. 1605 Navigation Nightmare
  7. 1612 Cube Stacking
  8. 3336 数据结构；并查集

其他

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。

在这里插入图片描述