所在小组
第五组
组内昵称
陈松彬
心得体会
Chapter3 section2
Author: @陈松彬
Date: 2020-10-18
section2 主要是3.8 ~ 3.12
一、GCC对数组访问的优化
书中给出的公式:对于数组T D[R][C],元素D[i][j]的内存地址为&D[i][j] = 数组起始地址 + i * C + j
贴出书中一个例子:
# define N 16
typedef int fix_matrix[N][N]
// 计算矩阵A的第i行跟 矩阵B的第k列 的向量积
int fix_prod_ele(fix_matrix A, fix_matrix B, long i, long k) {
long j;
int result = 0;
for (j=0; j<N; j++){
result += A[i][j] * B[j][k];
}
return result;
}
按照我们写的代码:每次循环总共会有3个乘法操作:
- 计算元素A[i][j]的地址 = A的起始地址 + i * N + j
- 计算元素B[j][k]的地址 = B的起始地址 + j * N + k
- A[i][j] * B[j][k]
不使用gcc优化:
gcc -Og -S fix_prod_ele_opt.c -o Og.s
使用gcc优化:
gcc -O1 -S fix_prod_ele_opt.c -o o1.s
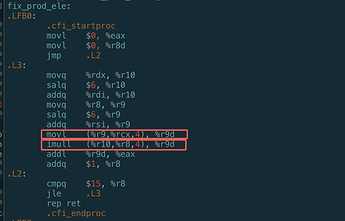
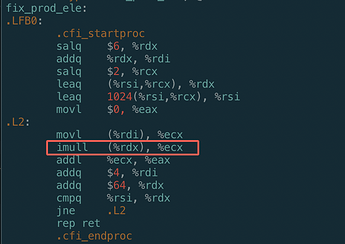
优化过后汇编代码:
a) 我们可以看到循环只用了一个乘法指令
b) 可以看到对于数组元素访问,本来是需要用到乘法计算数组元素地址的,结果都被GCC优化掉了,改成通过将地址加一个常量:
- addq $4, %rdi # Aptr ++
- addq $64, %rdx # Bptr += N
c) 再次证明乘法操作是比较耗时的,GCC编译器会千方百计减少乘法操作
二、数据对齐
-
地址必须是某个值K的倍数,这个K
-
为什么需要内存对齐:提高CPU从内存获取数据的效率
-
应用:
a) 利用内存对齐,通过对结构体中的某些字段的顺序进行重新排序,可以减少padding,进而使得一个结构体占用的内存减小。b) 这个优化貌似编译器不会帮我们做,我们可以写一个脚本,可以对我们的定义的结构体的字段进行重新排序。这个算法也很简单,只要把占用字节数多的字段排在前面即可。
c)比如
# 16字节 type TestStruc struct { A int # 0 B char # 4 C int # 8 D char # 12 } # 12字节 type TestStruc struct { A int 0 C int 4 B char 8 D char 9 } -
疑问1: 对于一个指令movb 内存,到寄存器;是如何传输的?
猜想:
(1)CPU执行指令,movb 内存地址,某个寄存器
(2)根据内存地址 找CPU cache 【这个是如何映射的?】
(3.1 )如果命中CPU cache
(3.2) 如果没有命中CPU Cache,从内存加载数据到CPU Cache
-
疑问2: 对于读下面中蓝色的8字节数据:
a) 为什么要执行两次内存操作(1)0-7(2)8-15
b) 为什么不能一次性搞定:3-10
三、SIMD指令
- SIMD 单指令多数据,也就是说同一个指令可以对多个数据进行操作。eg: 对于向量x = (1,1,1,1); y=(2,2,2,2),对于普通指令,需要执行四次加法操作,使用SIMD指令只需1个指令完成操作,x + y = (1,1,1,1)+(2,2,2,2) = (3,3,3,3)
- 发展路径:MMX → SSE → AVX
- 这些指令具有特殊的寄存器,寄存器存储大小不断变大,从最早的 64位 → 128位 → 256位 → 512位
- 在2000年Pentium中引入了SSE2,开始使用这些寄存器,支持浮点计算与操作