TalkGo算法之美第五期

算法之美
21

完美解决，谢谢大佬

func longestPalindrome(s string) string {
	res := ""
	for i := 0; i < len(s); i++ {
		for l, r := i, i; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
			if len(res) < r-l+1 {
				res = s[l : r+1]
			}
		}
		for l, r := i, i+1; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
			if len(res) < r-l+1 {
				res = s[l : r+1]
			}
		}
	}
	return res
}
22

方法一：（暴力枚举） O(n^2)

由于字符串长度小于1000，因此我们可以用 O(n^2)的算法枚举所有可能的情况。
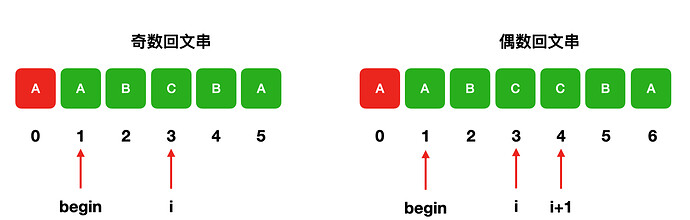
首先枚举回文串的中心 i，然后分两种情况向两边扩展边界，直到遇到不同字符为止:

回文串长度是奇数，则依次判断 s[i−k]==s[i+k],k=1,2,3,…
回文串长度是偶数，则依次判断 s[i−k]==s[i+k−1],k=1,2,3,…
如果遇到不同字符，则我们就找到了以 i 为中心的回文串边界。

时间复杂度分析：一共两重循环，所以时间复杂度是 O(n^2)

func longestPalindrome(s string) string {
	res := ""
	for i := 0; i < len(s); i++ {
		for l, r := i, i; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
			if len(res) < r-l+1 {
				res = s[l : r+1]
			}
		}
		for l, r := i, i+1; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
			if len(res) < r-l+1 {
				res = s[l : r+1]
			}
		}
	}
	return res
}

方法二：中心扩展算法

截屏2021-04-02 11.43.48.png
截屏2021-04-02 11.43.48.png2028×648 155 KB 

func longestPalindrome(s string) string {
	low, maxLen := 0, 0
	for i := range s {
		expand(s, i, i, &low, &maxLen)
		expand(s, i, i+1, &low, &maxLen)
	}
	return s[low : low+maxLen]
}
func expand(s string, l, r int, low, maxLen *int) {
	for ; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
	}
	if *maxLen < r-l-1 {
		*low = l + 1
		*maxLen = r - l - 1
	}
}

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是字符串的长度。长度为 1 和 2 的回文中心分别有 n 和 n−1 个，每个回文中心最多会向外扩展 O(n) 次。
  • 空间复杂度：O(1)。
func longestPalindrome(s string) string {
	start, end := 0, 0
	for i := range s {
		l, r := expand(s, i, i)
		if end-start < r-l {
			start, end = l, r
		}
		l, r = expand(s, i, i+1)
		if end-start < r-l {
			start, end = l, r
		}
	}
	return s[start : end+1]
}
func expand(s string, l, r int) (int, int) {
	for ; l >= 0 && r < len(s) && s[l] == s[r]; l, r = l-1, r+1 {
	}
	return l + 1, r - 1
}
23

图画得这么好的，用什么画的。

24

谢谢夸奖，图是用 ppt (keynote讲稿) 画得

25

只要工具用得好，没有不出活的:+1:

1 个赞