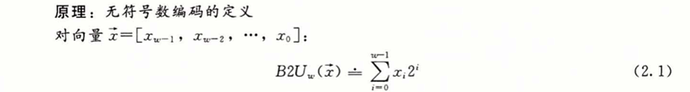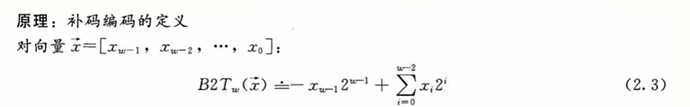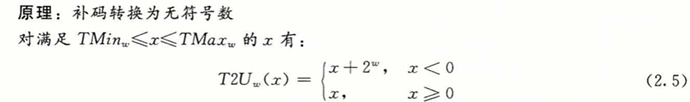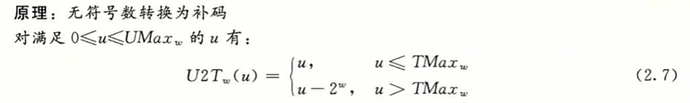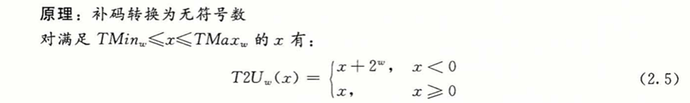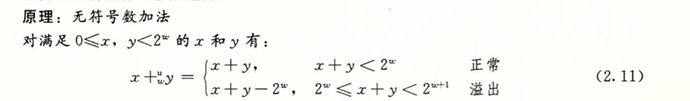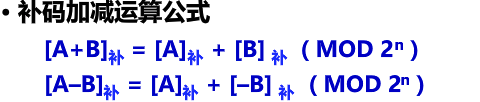所在小组:六组
组内昵称:杨凯伟
整数编码
向量 x 中的每一个元素表示一个二进制位,其中每一位取值为0或1。即我们理解的二进制转十进制的方法。
B2U_w(x) = \sum^{w-1}_{i=0} x_i2_i = x_{w-1} \cdot 2^{w-1} + x_{w-2} \cdot 2^{w-2} + ...+ x_0 \cdot 2^0
有符号数的最高有效位即为符号位,它的权重为 -2^{w-1}, 1时为负,0时为非负。由于 0 是非负数,这就导致能表示的整数比负数少一个。
B2U_w(x) = - x_{w-1}2^{w-1} + \sum^{w-1}_{i=0} x_i2_i =
- x_{w-1}2^{w-1} + x_{w-2} \cdot 2^{w-2} + x_{w-2} \cdot 2^{w-2} + ...+ x_0 \cdot 2^0
如:
B2T_4([1111]) = -1 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = -8 + 4 + 2+ 1 = -1
值得注意的是 -1 都是补码表示都是一个全1的串,然而这无符号数的最大值的表示一致。
正数用原码负数用补码。
计算机都用补码存储数据。
这两个说法都没有问题,因为正数的 原码 = 补码。
原因之一就是方便计算,如$165 + (-165) = 0$ 如果使用原码进行计算,需要单独把符号位拿出来,再做减法运算,而把符号位区分出来是需要额外的硬件电路支撑的,这很不方便。
如果使用补码,如下所示(这里按照16位进行举例):
0000 0000 1010 0101 + 1111 1111 0101 1011=0000 0000 0000 0000;
使用补码参与运算后,无需再管符号位,可以让符号位直接参与运算。
有符号数和无符号数的转换
原则:保持位值不变,只改变解释这些位的方式
先来看 C 语言中的强制转换:
short int v = -12345;
unsigned short uv = (unsigned short) v;
printf("v = %d, uv = %u\n", v, uv)
在采用补码的机器上(基本上计算机都采用补码存储信息)输出:v = -12345, uv=53191
原因:
-12345: 1100 1111 1100 0111
53191: 1100 1111 1100 0111
- 有符号数转无符号数
x >= 0 时结果不变,x < 0时结果为 x+2^w
- 无符号数转有符号数
对于小的数($<= TMax_w$)时结果不变,对于大的数($> TMax_w$)时,数字将被转换为一个负数。结果为 $u-2^w$。
在 C 语言中,当执行一个运算时,如果它的一个运算书是有符号的而另一个是无符号的,那么 C 语言会隐式地将有符号参数强制类型转换为无符号数。
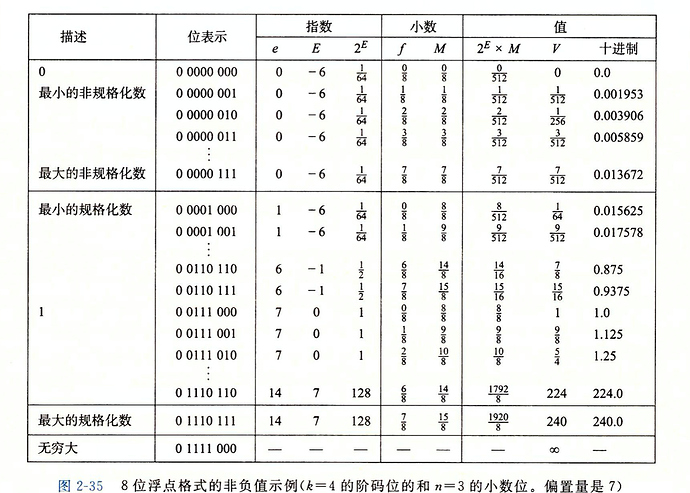
IEEE浮点数
讨论占用32位机器上的IEEE 754标准的单精度浮点数格式
IEEE754 标准把 float 型的32个坑做了如下划分:

其中包含了1位符号位S,8位阶码E和23位尾数M。
S: 符号位,0表示正数,1表示负数
E: E=e(实际指数)+127(Bais,值为 $2^{k-1} -1$)
M: 真正的有效位数包括二进制点右边的23个小数位和值为1 的隐式前导位(二进制点的左边),除非指数存储为全零。因此,有效格式中仅出现有效数字的23个小数位,但总精度为24位
IEEE754 标准做了这样的规定:当尾数(小数)不为0时,尾数域的最高有效位为1,即 ${\displaystyle (1.x_{1}x_{2}…x_{23})_{2}\times 2^{e}}$,规格化之后我们只需要存储一个尾数(即小数部分(frac),整数部分恒为1)和指数部分(exp)。
- 为什么要用指数加上127,才是阶码E,而不是直接用指数存进去?
我们希望存储到机器里的阶码永远都是正值,因为我们不希望再浪费一个坑去保存阶码的正负号,于是乎,干脆把指数加上127,而指数能取到的最小值就是-127,这样就可以保证阶码 E 永远都是正数啦,我们就不用再考虑指数正负号的问题了。
- 精度问题
十进制小数转化为二进制小数时,小数部分超过了 23 位就会发生精度丢失(舍入)。 默认是舍入到最接近的值,如果“舍”和“入”一样接近,那么取结果为偶数的选择。
浮点数计算时可能还会再次丢失精度。